CF704B Ant Man
题目描述
斯科特·朗正在与达伦·克罗斯作战。在他们所在的大厅里有 $n$ 把椅子,从左到右编号为 $1,2,...,n$。第 $i$ 把椅子位于坐标 $x_{i}$。斯科特现在在第 $s$ 把椅子上,克罗斯在第 $e$ 把椅子上。斯科特可以跳到所有其它椅子(不仅仅是相邻椅子)。他想从自己的位置(第 $s$ 把椅子)出发,恰好访问每把椅子一次,并最终在第 $e$ 把椅子上与克罗斯会合。
众所周知,斯科特可以缩小或变大(仅能变回正常大小),所以任意时刻他可以是小或大(正常)状态。注意,他只能在椅子上进行缩小或变大(不能在空中变身)。跳跃需要时间,但变大或缩小不耗时。从第 $i$ 把椅子跳到第 $j$ 把椅子需要 $|x_{i}-x_{j}|$ 秒。此外,跳离椅子和落到椅子时还需要额外时间。
如果斯科特要跳向左侧的椅子,他只能是小状态;如果要跳向右侧的椅子,他必须是大(正常)状态。
从第 $i$ 把椅子跳离需要:
- 若他为小状态,需额外 $c_{i}$ 秒。
- 否则(即为大状态),需额外 $d_{i}$ 秒。
落到第 $i$ 把椅子需要:
- 若他为小状态,需额外 $b_{i}$ 秒。
- 否则(即为大状态),需额外 $a_{i}$ 秒。
简而言之,从 $i$ 跳到 $j$ 需要:
- 若 $ji$,则耗时 $|x_{i}-x_{j}|+d_{i}+a_{j}$ 秒。
给定 $x$、$a$、$b$、$c$、$d$ 的值,找到斯科特到达克罗斯且恰好访问每把椅子一次的最短所需时间。
输入格式
输入的第一行为三个整数 $n,s,e$($2 \le n \le 5000, 1 \le s,e \le n, s \ne e$)——椅子的总数、斯科特的起始位置和目标位置。
第二行为 $n$ 个整数 $x_{1},x_{2},...,x_{n}$($1 \le x_{1} < x_{2} < \cdots < x_{n} \le 10^{9}$)。
第三行为 $n$ 个整数 $a_{1},a_{2},...,a_{n}$($1 \le a_{i} \le 10^{9}$)。
第四行为 $n$ 个整数 $b_{1},b_{2},...,b_{n}$($1 \le b_{i} \le 10^{9}$)。
第五行为 $n$ 个整数 $c_{1},c_{2},...,c_{n}$($1 \le c_{i} \le 10^{9}$)。
第六行为 $n$ 个整数 $d_{1},d_{2},...,d_{n}$($1 \le d_{i} \le 10^{9}$)。
输出格式
输出斯科特到达克罗斯且恰好访问每把椅子一次所需的最短时间。
说明/提示
在样例测试中,最优方案如下图所示:
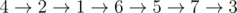
所耗时间为 $17+24+23+20+33+22=139$。
由 ChatGPT 5 翻译