CF707B Bakery

Masha wants to open her own bakery and bake muffins in one of the $ n $ cities numbered from $ 1 $ to $ n $ . There are $ m $ bidirectional roads, each of whose connects some pair of cities. To bake muffins in her bakery, Masha needs to establish flour supply from some storage. There are only $ k $ storages, located in different cities numbered $ a_{1},a_{2},...,a_{k} $ . Unforunately the law of the country Masha lives in prohibits opening bakery in any of the cities which has storage located in it. She can open it only in one of another $ n-k $ cities, and, of course, flour delivery should be paid — for every kilometer of path between storage and bakery Masha should pay $ 1 $ ruble. Formally, Masha will pay $ x $ roubles, if she will open the bakery in some city $ b $ ( $ a_{i}≠b $ for every $ 1

The first line of the input contains three integers $ n $ , $ m $ and $ k (1 \le n,m \le 10^{5} $ , $ 0 \le k \le n )$ — the number of cities in country Masha lives in, the number of roads between them and the number of flour storages respectively. Then $ m $ lines follow. Each of them contains three integers $ u $ , $ v $ and $ l(1 \le u,v \le n $ , $ 1 \le l \le 10^{9} $ , $ u \neq v )$ meaning that there is a road between cities $ u $ and $ v $ of length of $ l $ kilometers . If $ k\gt0 $ , then the last line of the input contains $ k $ distinct integers $ a_{1},a_{2},\dots,a_{k} (1 \le a_{i} \le n)$ — the number of cities having flour storage located in. If $ k=0 $ then this line is not presented in the input.

Print the minimum possible amount of rubles Masha should pay for flour delivery in the only line. If the bakery can not be opened (while satisfying conditions) in any of the $ n $ cities, print $ -1 $ in the only line.

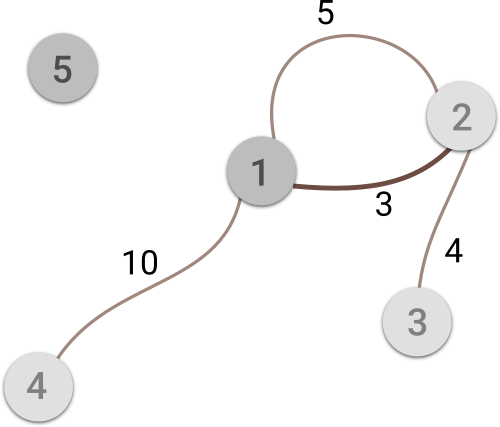Image illustrates the first sample case. Cities with storage located in and the road representing the answer are darkened.