CF707D Persistent Bookcase

最近在学校，Alina 学会了什么是可持久化数据结构：即每次修改时，数据结构总能保留之前的版本，并可随时访问这些旧版本。 回到家后，Alina 决定发明属于自己的可持久化数据结构。发明过程很快，毕竟她的床边正好有个书架。Alina 认为书架就是很好的可持久化数据结构。最开始，书架是空的，也就是说每一层的每一个位置都没有书。 这个书架由 $n$ 层组成，每一层正好有 $m$ 个放书的位置。Alina 用 $1$ 到 $n$ 的整数为书架的层数编号，某层内部的位置编号用 $1$ 到 $m$ 表示。起始时，书架都是空的，即所有位置上都没有书。 Alina 记录下 $q$ 个操作，将依次施加在书架上。每个操作属于以下四种中的一种： - $1\ i\ j$ —— 如果第 $i$ 层第 $j$ 个位置没有书，则在此处放一本书。 - $2\ i\ j$ —— 如果第 $i$ 层第 $j$ 个位置有书，则将其移走。 - $3\ i$ —— 翻转第 $i$ 层所有位置的放书状态：有书的拿掉，没书的放一本。 - $4\ k$ —— 将书架恢复到执行完第 $k$ 个操作后的状态。特别地，$k=0$ 表示恢复到最初状态（完全空书架）。 每执行一次操作后，Alina 都感兴趣于当前书架上书的总数。Alina 在学校得了“A”，所以她毫无难度地解决了这个问题。那么你呢？

输入的第一行为三个整数 $n$、$m$ 和 $q$（$1 \leq n, m \leq 10^{3}$，$1 \leq q \leq 10^{5}$），分别表示书架的层数、每层位置数和操作数。 接下来的 $q$ 行，每行描述一个操作，按照时间顺序给出，格式如题目描述中的四种情况之一。 保证所有层号和位置号都在有效范围内，第四种操作中参数 $k$ 要么是 $0$（即初态），要么为之前某个操作的编号。

对于每个操作，依次输出操作后书架上的书的总数，各占一行，顺序与操作给出顺序一致。

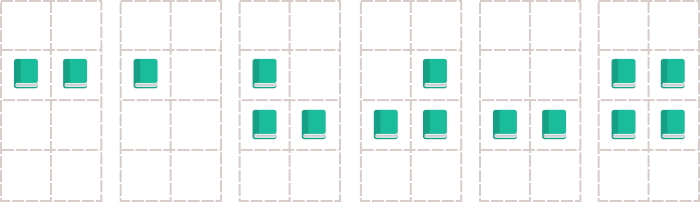
 此图片展示了第二个样例的情况。 由 ChatGPT 5 翻译