CF711D Directed Roads

ZS the Coder 和 Chris the Baboon 在 Udayland 探险了很长时间。他们发现 Udayland 由 $n$ 个城镇组成，编号从 $1$ 到 $n$。 Udayland 有 $n$ 条有向道路，第 $i$ 条道路连接城镇 $i$ 和某个其他城镇 $a_{i}$（$a_{i} \ne i$）。ZS the Coder 可以任意翻转任何一条道路的方向，即如果某条路原本从城镇 $A$ 到城镇 $B$，那么翻转后就会从 $B$ 到 $A$。 如果存在一组不同的城镇 $A_1, A_2, \ldots, A_k$（$k > 1$），使得对于每个 $1 \le i < k$ 都有一条从 $A_i$ 到 $A_{i+1}$ 的道路，并且还有一条从 $A_k$ 到 $A_1$ 的道路，则 ZS the Coder 认为这些道路是“令人困惑”的。换句话说，如果某些道路形成了若干城镇的有向环路，那么这些道路就是令人困惑的。 现在 ZS the Coder 想知道，在初始设置下，可以选择多少种道路的集合（共 $2^n$ 种方案），将这些集合中的每条道路恰好翻转一次后，最终的道路网络不会令人困惑。 注意，翻转之后可能会出现某个城镇有多条出边，也可能有城镇没有任何出边，或者某对城镇之间有多条道路。 请问有多少种方案可以翻转部分道路，使得最终道路网络不包含有向环。由于结果可能过大，请输出结果对 $10^9+7$ 取模后的值。

第一行包含一个整数 $n$（$2 \le n \le 2 \times 10^5$），表示 Udayland 的城镇数量。 第二行包含 $n$ 个整数 $a_1,a_2,\ldots,a_n$（$1 \le a_i \le n,$ $a_i\ne i$），其中 $a_i$ 表示第 $i$ 条道路从城镇 $i$ 指向城镇 $a_i$。

输出一个整数，表示有多少种方法可以选择部分道路进行翻转，使得最终所有道路不包含有向环。由于答案可能过大，请输出其对 $10^9+7$ 取模后的结果。

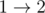
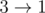
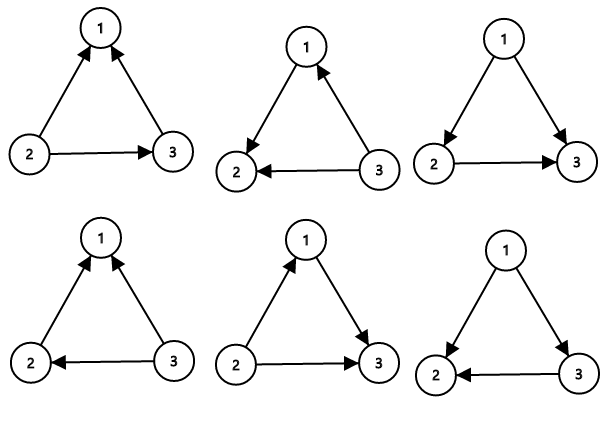
以第一个样例为例。有 $3$ 个城镇和 $3$ 条道路，城镇编号从 $1$ 到 $3$，道路分别如图：    将道路编号为 $1$ 到 $3$。 能够使网络不困惑的翻转道路集合为 $\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\}$。注意，空集是不合法的，因为如果不翻转任何道路则 $1,2,3$ 之间会形成有向环，因此是困惑的。同理，把所有道路都翻转也是困惑的情况。因此一共有 $6$ 种合法方案。 下图展示了第一个样例中所有可能的合理道路方向配置：  由 ChatGPT 5 翻译