CF712E Memory and Casinos

There are $ n $ casinos lined in a row. If Memory plays at casino $ i $ , he has probability $ p_{i} $ to win and move to the casino on the right ( $ i+1 $ ) or exit the row (if $ i=n $ ), and a probability $ 1-p_{i} $ to lose and move to the casino on the left ( $ i-1 $ ) or also exit the row (if $ i=1 $ ). We say that Memory dominates on the interval $ i...\ j $ if he completes a walk such that, - He starts on casino $ i $ . - He never looses in casino $ i $ . - He finishes his walk by winning in casino $ j $ . Note that Memory can still walk left of the $ 1 $ -st casino and right of the casino $ n $ and that always finishes the process. Now Memory has some requests, in one of the following forms: - $ 1 $ $ i $ $ a $ $ b $ : Set 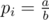. - $ 2 $ $ l $ $ r $ : Print the probability that Memory will dominate on the interval $ l...\ r $ , i.e. compute the probability that Memory will first leave the segment $ l...\ r $ after winning at casino $ r $ , if she starts in casino $ l $ . It is guaranteed that at any moment of time $ p $ is a non-decreasing sequence, i.e. $ p_{i}

The first line of the input contains two integers $ n $ and $ q $ ( $ 1

Print a real number for every request of type $ 2 $ — the probability that boy will "dominate" on that interval. Your answer will be considered correct if its absolute error does not exceed $ 10^{-4} $ . Namely: let's assume that one of your answers is $ a $ , and the corresponding answer of the jury is $ b $ . The checker program will consider your answer correct if $ |a-b|