CF715A Plus and Square Root

ZS the Coder 正在玩一个游戏。屏幕上显示着一个数字，并有两个按钮，‘ $ + $ ’（加号）和‘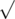’（平方根号）。最初，屏幕上显示的数字是 $ 2 $。游戏一共有 $ n+1 $ 个关卡，ZS the Coder 从第 $ 1 $ 关开始。 当 ZS the Coder 处于第 $ k $ 关时，他可以进行以下操作： 1. 按下‘ $ + $ ’按钮。这样会使屏幕上的数字增加 $ k $，即如果当前屏幕上的数字为 $ x $，那么它将变为 $ x+k $。 2. 按下‘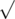’按钮。若屏幕上的数字为 $ x $，按下该按钮后，数字将变为 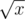。之后，ZS the Coder 升级，当前关卡变为 $ k+1 $。只有当 $ x $ 是一个完全平方数，即 $ x=m^2 $ （$ m $ 是正整数）时才能按下该按钮。 此外，每次操作后，如果 ZS the Coder 正在第 $ k $ 关，且屏幕上的数字为 $ m $，则 $ m $ 必须是 $ k $ 的倍数。注意，这个条件只在完成某一次按键操作后检查。例如，如果 ZS the Coder 正在第 $ 4 $ 关，当前数字为 $ 100 $，他按下‘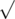’按钮，数字变为 $ 10 $。注意此时 $ 10 $ 不能被 $ 4 $ 整除，但操作仍然有效，因为这时他已经在第 $ 5 $ 关，且 $ 10 $ 能被 $ 5 $ 整除。 现在，ZS the Coder 需要你的帮助来通关——也就是让他到达第 $ n+1 $ 关。换句话说，他需要在第 $ i $ 关分别按下‘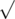’ 按钮 $ n $ 次。请你帮助他确定，在每一关按下平方根按钮前，应按多少次‘ $ + $ ’按钮。 请注意，ZS the Coder 只需要找到任意一组能过关的操作顺序即可，不一定要最优化操作次数。

输入只有一行，一个整数 $ n $（$ 1 \leq n \leq 100000 $），表示 ZS the Coder 需要到达第 $ n+1 $ 关。

输出 $ n $ 个非负整数，每行一个。第 $ i $ 个数表示在第 $ i $ 关按下‘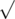’按钮前，需要按多少次‘ $ + $ ’按钮。 输出的每个数字都不应超过 $ 10^{18} $。屏幕上的数字可以超过 $ 10^{18} $。 保证至少存在一种解。如果有多种方案，输出任意一种即可。

在第一个样例中： 第一级，ZS the Coder 按下‘ $ + $ ’按钮 $ 14 $ 次（初始数字为 $ 2 $），屏幕上的数字变为 $ 2+14 \cdot 1=16 $。随后按下平方根按钮，数字变为 $ \sqrt{16}=4 $。 接着，在第二级，ZS 按下‘ $ + $ ’按钮 $ 16 $ 次，数字变成 $ 4+16 \cdot 2=36 $。然后按下平方根按钮，数字变为 $ \sqrt{36}=6 $。 之后，在第三级，ZS 按下‘ $ + $ ’按钮 $ 46 $ 次，数字变为 $ 6+46 \cdot 3=144 $。随后按下平方根按钮，数字变为 $ \sqrt{144}=12 $。 请注意，$ 12 $ 是 $ 4 $ 的倍数，因此 ZS the Coder 可以到达第 $ 4 $ 关。 又如，第三级如果按 $ 10 $ 次‘ $ + $ ’按钮，数字会变为 $ 6+10\cdot 3=36 $，再按下平方根按钮后为 $ 6 $。但此时 $ 6 $ 不能被 $ 4 $ 整除，所以这样的方案不合法。 在第二个样例中： 第一级，ZS the Coder 按 $ 999999999999999998 $ 次‘ $ + $ ’按钮（初始数字为 $ 2 $），数字变为 $ 2+999999999999999998\cdot 1=10^{18} $。按下平方根按钮后数字为 $ 10^{9} $。 然后，在第二级，ZS 按 $ 44500000000 $ 次‘ $ + $ ’按钮，数字为 $ 10^{9} + 44500000000\cdot 2 = 9\cdot 10^{10} $，按下平方根按钮后为 $ 300000 $。 注意 $ 300000 $ 是 $ 3 $ 的倍数，所以 ZS the Coder 能到达第 $ 3 $ 关。 由 ChatGPT 5 翻译