CF715A Plus and Square Root

ZS the Coder is playing a game. There is a number displayed on the screen and there are two buttons, ' $ + $ ' (plus) and '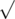' (square root). Initially, the number $ 2 $ is displayed on the screen. There are $ n+1 $ levels in the game and ZS the Coder start at the level $ 1 $ . When ZS the Coder is at level $ k $ , he can : 1. Press the ' $ + $ ' button. This increases the number on the screen by exactly $ k $ . So, if the number on the screen was $ x $ , it becomes $ x+k $ . 2. Press the '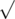' button. Let the number on the screen be $ x $ . After pressing this button, the number becomes 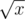. After that, ZS the Coder levels up, so his current level becomes $ k+1 $ . This button can only be pressed when $ x $ is a perfect square, i.e. $ x=m^{2} $ for some positive integer $ m $ . Additionally, after each move, if ZS the Coder is at level $ k $ , and the number on the screen is $ m $ , then $ m $ must be a multiple of $ k $ . Note that this condition is only checked after performing the press. For example, if ZS the Coder is at level $ 4 $ and current number is $ 100 $ , he presses the '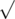' button and the number turns into $ 10 $ . Note that at this moment, $ 10 $ is not divisible by $ 4 $ , but this press is still valid, because after it, ZS the Coder is at level $ 5 $ , and $ 10 $ is divisible by $ 5 $ . ZS the Coder needs your help in beating the game — he wants to reach level $ n+1 $ . In other words, he needs to press the '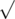' button $ n $ times. Help him determine the number of times he should press the ' $ + $ ' button before pressing the '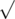' button at each level. Please note that ZS the Coder wants to find just any sequence of presses allowing him to reach level $ n+1 $ , but not necessarily a sequence minimizing the number of presses.

The first and only line of the input contains a single integer $ n $ ( $ 1

Print $ n $ non-negative integers, one per line. $ i $ -th of them should be equal to the number of times that ZS the Coder needs to press the ' $ + $ ' button before pressing the '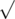' button at level $ i $ . Each number in the output should not exceed $ 10^{18} $ . However, the number on the screen can be greater than $ 10^{18} $ . It is guaranteed that at least one solution exists. If there are multiple solutions, print any of them.

In the first sample case: On the first level, ZS the Coder pressed the ' $ + $ ' button $ 14 $ times (and the number on screen is initially $ 2 $ ), so the number became $ 2+14·1=16 $ . Then, ZS the Coder pressed the '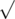' button, and the number became 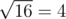. After that, on the second level, ZS pressed the ' $ + $ ' button $ 16 $ times, so the number becomes $ 4+16·2=36 $ . Then, ZS pressed the '' button, levelling up and changing the number into 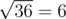. After that, on the third level, ZS pressed the ' $ + $ ' button $ 46 $ times, so the number becomes $ 6+46·3=144 $ . Then, ZS pressed the '' button, levelling up and changing the number into 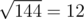. Note that $ 12 $ is indeed divisible by $ 4 $ , so ZS the Coder can reach level $ 4 $ . Also, note that pressing the ' $ + $ ' button $ 10 $ times on the third level before levelling up does not work, because the number becomes $ 6+10·3=36 $ , and when the '' button is pressed, the number becomes 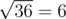 and ZS the Coder is at Level $ 4 $ . However, $ 6 $ is not divisible by $ 4 $ now, so this is not a valid solution. In the second sample case: On the first level, ZS the Coder pressed the ' $ + $ ' button $ 999999999999999998 $ times (and the number on screen is initially $ 2 $ ), so the number became $ 2+999999999999999998·1=10^{18} $ . Then, ZS the Coder pressed the '' button, and the number became 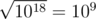. After that, on the second level, ZS pressed the ' $ + $ ' button $ 44500000000 $ times, so the number becomes $ 10^{9}+44500000000·2=9·10^{10} $ . Then, ZS pressed the '' button, levelling up and changing the number into 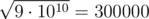. Note that $ 300000 $ is a multiple of $ 3 $ , so ZS the Coder can reach level $ 3 $ .