CF715B Complete The Graph

ZS the Coder 画了一张无向图，这张图有 $n$ 个顶点，编号从 $0$ 到 $n-1$，以及 $m$ 条边。每条边都有一个权值，且权值为正整数。 第二天，ZS the Coder 发现有些边的权值被擦掉了！现在他想重新为这些权值被擦掉的边分配一个正整数权值，使得最终图中从顶点 $s$ 到顶点 $t$ 的最短路长度恰好为 $L$。你能帮帮他吗？

第一行包含五个整数 $n,m,L,s,t$（$2\leq n\leq 1000, 1\leq m\leq 10000, 1\leq L\leq 10^{9}, 0\leq s,t\leq n-1, s\neq t$），分别表示顶点个数、边数、期望的最短路长度、起点和终点的编号。 接下来的 $m$ 行描述图中的每一条边。第 $i$ 行包含三个整数 $u_{i}, v_{i}, w_{i}$（$0\leq u_{i}, v_{i} \leq n-1, u_{i}\neq v_{i}, 0\leq w_{i}\leq 10^{9}$）。$u_{i}$ 和 $v_{i}$ 表示边的两个端点，$w_{i}$ 表示这条边的权值。如果 $w_{i}=0$，说明这条边的权值被擦掉了。 保证任意一对顶点之间至多有一条边。

如果无法分配权值使得最短路长度等于 $L$，输出一行 "NO"（不带引号）。 否则，第一行输出 "YES"（不带引号）。接下来 $m$ 行，每行包含三个整数 $u_{i}, v_{i}, w_{i}$，表示一条边，$w_{i}$ 为给这条边分配的权值。输出的边与输入的图应完全一致，未被擦掉的权值应保持不变，被擦掉的权值可以为任意正整数，且不超过 $10^{18}$。 边的输出顺序任意。从 $s$ 到 $t$ 的最短路长度必须等于 $L$。 如果有多组方案，输出任意一组即可。

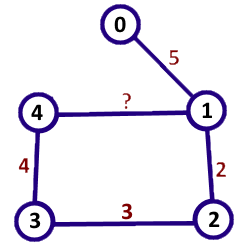
下图展示了第一个样例的数据情况：  在第一个样例中，只有一条边的权值缺失。将其赋值为 $8$，可以使 $0$ 到 $4$ 的最短路长度为 $13$。 在第二个样例中，图中仅有一条边。显然，唯一的办法是将擦掉的权值赋为 $123456789$。 在最后一个样例中，没有可以分配的权值，但最短路长度不等于要求值，因此答案为 "NO"。 由 ChatGPT 5 翻译