CF715E Complete the Permutations

ZS the Coder 拥有两个排列 $p$ 和 $q$，它们是 $ \{1,2,\ldots,n\} $ 的排列，但其中部分元素被替换为 $0$。排列 $p$ 和 $q$ 之间的距离被定义为将 $p$ 变换为 $q$ 所需的最少移动次数，每次移动的操作是交换 $p$ 中恰好两个元素的位置。 ZS the Coder 想要确定用 $ \{1,2,\ldots,n\} $ 中的正整数替换零，使得 $p$ 和 $q$ 均为 $ \{1,2,\ldots,n\} $ 的排列，并且 $p$ 和 $q$ 间的距离恰好为 $k$ 的方案数。 ZS the Coder 想要你帮助他求出所有 $0 \leq k \leq n-1$ 时的答案。

输入的第一行为一个整数 $n$（$1 \leq n \leq 250$），表示排列中元素的数量。 第二行包含 $n$ 个整数，$p_1, p_2, \ldots, p_n$（$0 \leq p_i \leq n$），表示排列 $p$。保证至少有一种用正整数替换 $0$ 的方案使得 $p$ 是 $ \{1,2,\ldots,n\} $ 的排列。 第三行包含 $n$ 个整数，$q_1, q_2, \ldots, q_n$（$0 \leq q_i \leq n$），表示排列 $q$。保证至少存在一种用正整数替换 $0$ 的方案使得 $q$ 是 $ \{1,2,\ldots,n\} $ 的排列。

输出 $n$ 个整数，第 $i$ 个整数表示 $k=i-1$ 时合法方案数。由于答案可能较大，请将答案对 $998244353=2^{23} \cdot 7 \cdot 17 + 1$ 取模后输出。

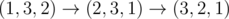在第一个样例中，只有一种方法可以替换 $0$，使得 $p$ 和 $q$ 一致，需要 $0$ 次交换，即 $p=(1,2,3), q=(1,2,3)$。 有两种方法替换 $0$，使得将 $p$ 变为 $q$ 恰好需要 $1$ 次交换。其中一种为 $p=(1,2,3), q=(3,2,1)$，交换 $p$ 中的 $1$ 和 $3$ 可以将其变为 $q$；另一种是 $p=(1,3,2), q=(1,2,3)$，交换 $p$ 中的 $2$ 和 $3$ 即可。 最后，有一种方法替换 $0$，使得将 $p$ 变为 $q$ 恰好需要 $2$ 次交换，即 $p=(1,3,2), q=(3,2,1)$。可以这样操作： 。 由 ChatGPT 5 翻译