CF717F Heroes of Making Magic III

我正悠闲地漫步在阳光下，啊-啊！这真是太棒了！我们的“造物英雄”们正在单向道路上悠然前行，与小魔怪们战斗。小魔怪是弱小无力的生物，他们几乎一无是处。然而，英雄们却很享受与小魔怪的战斗，哪怕只是为了乐趣。 我们的主角 Ignatius 非常喜欢小魔怪。他正在观察一排小魔怪，这排小魔怪被表示为一个长度为 $n$ 的从零开始编号的整数数组 $a$，其中 $a_i$ 表示第 $i$ 个位置上有多少只小魔怪。有时候，小魔怪还会莫名其妙地出现。当英雄们与小魔怪战斗时，他们会选择这排小魔怪上的一个连续区间，从区间的一端出发，在区间的另一端结束，并且不会离开这个区间。他们每次只能向左或向右移动一个格子，每当移动到一个新的格子上时，就会打败这格子上的一只小魔怪，因此这个格子上的小魔怪数量减少 $1$。英雄们在一开始进入区间时，同样要立刻打败一只小魔怪。 他们的目标是在不走到区间内空格子的情况下（即不能走到没有小魔怪的格子上），依次清空这个区间内的所有小魔怪。如果区间内的某个格子在移动到时已经没有小魔怪可打，英雄就会感到无聊，不会那样做了。虽然 Ignatius 很喜欢小魔怪，并不真的想打它们，所以在本题的事件中并没有小魔怪真正受伤。但他想知道，如果他愿意，是否有可能以上述方式清空某个区间内的所有小魔怪。 你会得到 $q$ 个询问，每个询问有两种类型： - $1\ a\ b\ k$ 表示区间 $[a, b]$ 上的每个格子都增加 $k$ 只小魔怪 - $2\ a\ b$ 询问是否可以按照上述方式清空区间 $[a, b]$ 上的所有小魔怪

第一行输入一个整数 $n$，表示数组 $a$ 的长度（$1 \leq n \leq 200\,000$）。 第二行输入 $n$ 个整数 $a_1, a_2, \ldots, a_n$，表示每个格子上最初有多少只小魔怪（$0 \leq a_i \leq 5000$）。 第三行输入一个整数 $q$（$1 \leq q \leq 300\,000$），表示查询个数。 接下来的 $q$ 行，每行表示一个查询。每个查询有两种形式： - $1\ a\ b\ k$，代表区间 $[a, b]$ 上每个格子增加 $k$ 只小魔怪 - $2\ a\ b$，查询是否可以按照题意清空区间 $[a, b]$ 其中 $0 \leq a \leq b < n$，$0 \leq k \leq 5000$。

对于每个第二种类型的查询，如果可以清空该区间，输出 $1$，否则输出 $0$。

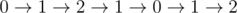
对于第一个查询，可以很容易验证，从第一个格子走到最后一个格子的过程中无法全部清空小魔怪。假如我们给第二个位置增加 $1$ 只小魔怪，就有可能清空这个区间。例如下面这样移动：  由 ChatGPT 5 翻译