CF718C Sasha and Array

Sasha has an array of integers $ a_{1},a_{2},...,a_{n} $ . You have to perform $ m $ queries. There might be queries of two types: 1. 1 l r x — increase all integers on the segment from $ l $ to $ r $ by values $ x $ ; 2. 2 l r — find 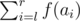, where $ f(x) $ is the $ x $ -th Fibonacci number. As this number may be large, you only have to find it modulo $ 10^{9}+7 $ . In this problem we define Fibonacci numbers as follows: $ f(1)=1 $ , $ f(2)=1 $ , $ f(x)=f(x-1)+f(x-2) $ for all $ x>2 $ . Sasha is a very talented boy and he managed to perform all queries in five seconds. Will you be able to write the program that performs as well as Sasha?

The first line of the input contains two integers $ n $ and $ m $ ( $ 1

For each query of the second type print the answer modulo $ 10^{9}+7 $ .

Initially, array $ a $ is equal to $ 1 $ , $ 1 $ , $ 2 $ , $ 1 $ , $ 1 $ . The answer for the first query of the second type is $ f(1)+f(1)+f(2)+f(1)+f(1)=1+1+1+1+1=5 $ . After the query 1 2 4 2 array $ a $ is equal to $ 1 $ , $ 3 $ , $ 4 $ , $ 3 $ , $ 1 $ . The answer for the second query of the second type is $ f(3)+f(4)+f(3)=2+3+2=7 $ . The answer for the third query of the second type is $ f(1)+f(3)+f(4)+f(3)+f(1)=1+2+3+2+1=9 $ .