CF720D Slalom
题目描述
小女孩 Masha 喜欢冬季运动,今天她打算参加高山滑雪。
赛道被表示为一个由 $n \times m$ 个方格组成的网格。赛道上有一些障碍物,这些障碍物呈矩形,由网格方格组成。Masha 必须从方格 $(1,1)$ 走到方格 $(n,m)$。她只能从一个方格走到相邻的方格:要么向右,要么向上。如果某个方格被障碍物占据,则不允许走到那个方格。
可以发现每个障碍物实际上有两种方式通过:它可能在 Masha 路径的右侧,也可能在路径的左侧。Masha 喜欢尝试所有的方式,所以她想知道通过赛道有多少种方法。如果对于同一个障碍物,在一种方案中它在路径右侧,而在另一种方案中它在路径左侧,则认为这两种方案是不同的。
请你帮助 Masha 计算通过赛道的方案数。由于答案可能很大,请你输出对 $10^9+7$ 取模后的结果。
下图展示了样例测试中不同的通过方式。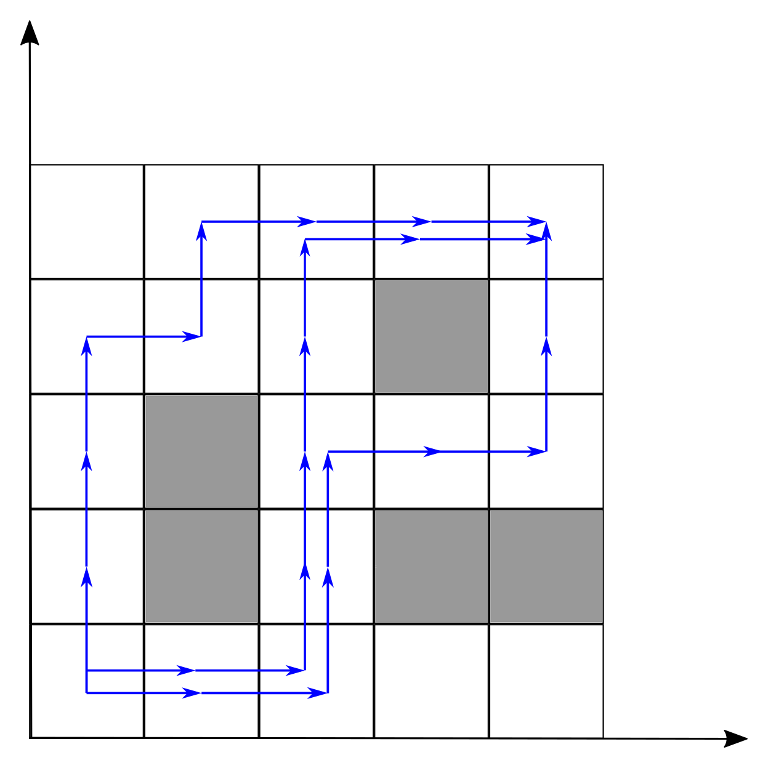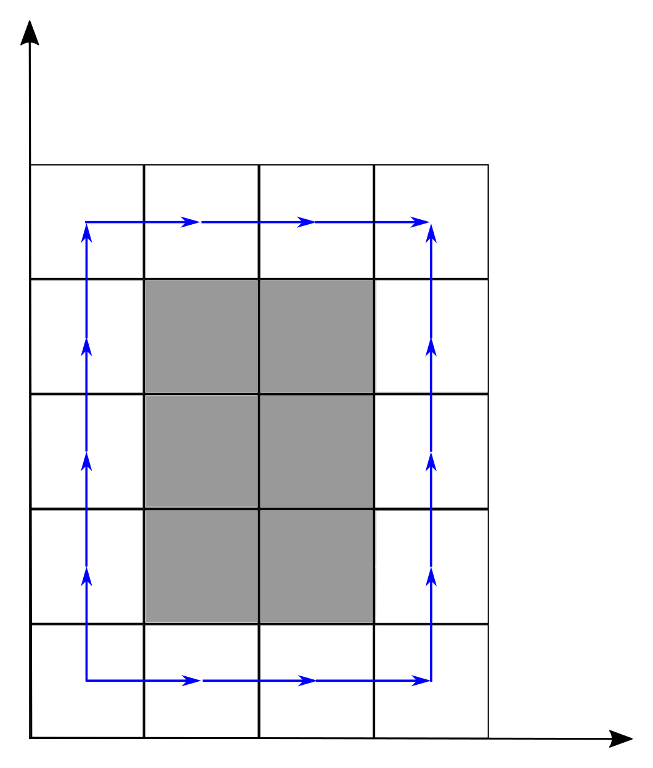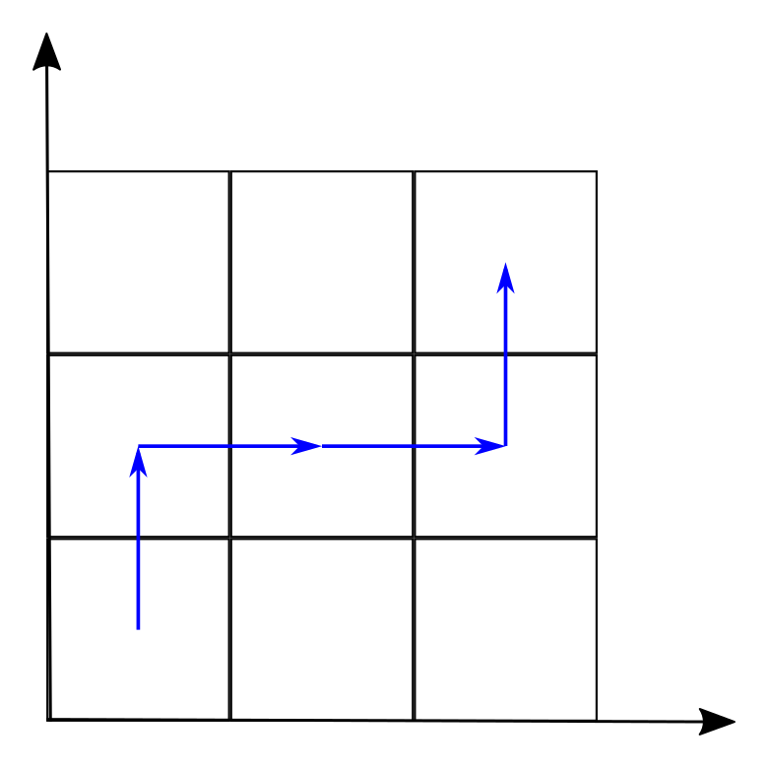
输入格式
输入的第一行为三个正整数:$n$、$m$ 和 $k$($3 \leq n, m \leq 10^6$,$0 \leq k \leq 10^5$)——表示赛道的大小和障碍物的数量。
接下来的 $k$ 行,每行包含四个正整数:$x_1$、$y_1$、$x_2$、$y_2$($1 \leq x_1 \leq x_2 \leq n$,$1 \leq y_1 \leq y_2 \leq m$)——表示障碍物的左下角和右上角的坐标。
保证在 $(1,1)$ 和 $(n,m)$ 这两个方格上没有障碍物,并且障碍物之间不会重叠(但可以接触)。
输出格式
输出一个整数,表示通过赛道的方案数,对 $10^9+7$ 取模。
说明/提示
由 ChatGPT 5 翻译