CF722E Research Rover

很遗憾，正式的题目描述太长了，这里直接给出传说背景。 研究探测车终于抵达了火星表面，准备完成它的任务。然而，由于导航系统设计失误，探测车处在了错误的位置。 探测车将在一个由 $n$ 行 $m$ 列组成的网格上运行。我们用 $(r, c)$ 表示第 $r$ 行第 $c$ 列的格子。从每个格子，探测车都可以移动到和当前位置相邻的任意格子（即上下左右相邻）。 探测车当前位于格子 $(1,1)$，它必须移动到格子 $(n, m)$。它会随机选择一条最短路径到达终点，每一种路径的可能性均等。 探测车的货舱里装有用于科研的电池。最初，电池的电量为 $s$ 单位能量。 有些格子中存在异常。每当探测车进入带有异常的格子时，电池的能量会损失一半（向下取整）。形式化地说，如果进入异常格子前电量为 $x$，则经过后电量变为 $\left\lfloor \frac{x}{2} \right\rfloor$。 由于探测车会随机选择一条最短路径前进，请计算它到达 $(n, m)$ 后电池电量的期望值。如果 $(1,1)$ 和 $(n, m)$ 格子中存在异常，也会影响电池能量。

输入的第一行包含四个整数 $n$、$m$、$k$ 和 $s$（$1\leq n, m\leq 100000$，$0\leq k\leq 2000$，$1\leq s\leq 1000000$），分别表示网格的行数、列数、有异常的格子数量，以及电池的初始电量。 接下来的 $k$ 行，每行包含两个整数 $r_i$ 和 $c_i$（$1\leq r_i\leq n$，$1\leq c_i\leq m$），表示存在异常的格子的坐标。保证每个格子至多被记录一次。

答案总可以表示为最简分数 $\frac{P}{Q}$。请输出唯一的整数 $P·Q^{-1}$（即 $P$ 乘以 $Q$ 的逆元），结果对 $10^9+7$ 取模。

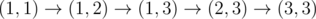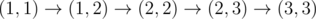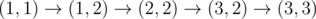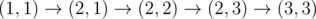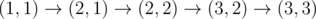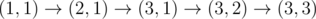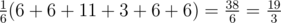在第一个样例中，探测车有如下六条路径： 1. ，经过格子 $(2,3)$ 后电量等于 $6$。 2. ，经过格子 $(2,3)$ 后电量等于 $6$。 3. ，电量保持不变，仍然是 $11$。 4. ，经过 $(2,1)$ 和 $(2,3)$ 后，电量依次变为 $6$ 与 $3$。 5. ，经过 $(2,1)$ 后电量等于 $6$。 6. ，经过 $(2,1)$ 后电量等于 $6$。 电池剩余电量的期望按以下公式计算： 。 因此 $P=19$，$Q=3$。 $3^{-1}$ 模 $10^{9}+7$ 等于 $333333336$。 $19·333333336=333333342 (\bmod 10^{9}+7)$。 由 ChatGPT 5 翻译