CF730F Ber Patio

Polycarp is a regular customer at the restaurant "Ber Patio". He likes having lunches there. "Ber Patio" has special discount program for regular customers. A customer can collect bonuses and partially cover expenses in the restaurant. Let's assume a customer currently has $ b $ bonuses and she has to pay $ r $ burles for a lunch. In this case the customer can use bonuses (1 bonus = 1 burle) to reduce the payment. She can cover at most half of the payment using bonuses. However, 1 bonus will be added to the customer's bonus balance per each 10 burles she paid. Formally: 1. a customer can choose any number $ x $ of bonuses to use (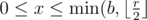)), 2. the customer's bonus balance is reduced by $ x $ , 3. the customer pays $ r-x $ burles, 4. the customer's bonus balance is increased by $ ⌊(r-x)/10⌋ $ (i.e. integer division rounded down is used). Initially, there are $ b $ bonuses on Polycarp's account. Polycarp is going to have a lunch in "Ber Patio" for the next $ n $ days. He estimated the values $ a_{1},a_{2},...,a_{n} $ , where $ a_{i} $ is the number of burles in a receipt for the $ i $ -th day. The sum over all receipts doesn't exceed $ 10^{5} $ burles. Write a program to find the minimum number of burles Polycarp has to spend and an optimal strategy to use bonuses.

The first line contains two integer numbers $ n $ and $ b $ ( $ 1

On the first line, print the expected minimal number of burles to pay for all $ n $ receipts. On the second line, print the sequence of integer numbers $ b_{1},b_{2},...,b_{n} $ , where $ b_{i} $ is the number of bonuses to use on the $ i $ -th day. If there are multiple solutions, print any of them.