CF734E Anton and Tree

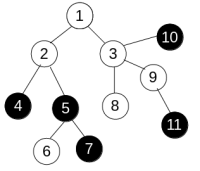
Anton 在他的花园里种了一棵树。如果你忘了的话，树是一种连通且无环的无向图。 这棵树有 $n$ 个顶点，每个顶点被涂成黑色或白色。Anton 不喜欢多种颜色的树，所以他想将整棵树变成同一种颜色（全黑或全白）。 为了改变颜色，Anton 只能使用一种操作。我们用 $paint(v)$ 表示这个操作，其中 $v$ 是树上的某个顶点。这个操作会改变所有顶点 $u$ 的颜色，满足从 $v$ 到 $u$ 的最短路径上的所有顶点（包括 $v$ 和 $u$）颜色都相同。例如，下图中：  对顶点 $3$ 执行 $paint(3)$ 操作后，变为如下：  Anton 想知道最少需要执行多少次操作，才能使所有顶点的颜色都一致。

输入的第一行是一个整数 $n$（$1 \leq n \leq 200000$），表示树中顶点的数量。 第二行包含 $n$ 个整数 $color_{i}$（$0 \leq color_{i} \leq 1$），表示每个顶点的颜色。$color_{i}=0$ 表示第 $i$ 个顶点初始为白色，$color_{i}=1$ 表示初始为黑色。 接下来有 $n-1$ 行，每行包含两个整数 $u_{i}$ 和 $v_{i}$（$1 \leq u_{i},v_{i} \leq n,u_{i} \neq v_{i}$），表示有一条边连接顶点 $u_{i}$ 和 $v_{i}$。保证所有的 $(u_i, v_i)$ 都不同，即没有重边。

输出一个整数，表示 Anton 至少需要多少次操作才能使整棵树颜色统一为黑色或白色。

对于第一个样例，树结构如图。如果我们先对顶点 $3$ 执行 $paint(3)$ 操作，再对顶点 $6$ 执行一次操作，整棵树就会变成全黑，因此答案为 $2$。 对于第二个样例，整棵树已经是全白，不需要操作，所以答案为 $0$。 由 ChatGPT 5 翻译