CF744B Hongcow's Game
Description
This is an interactive problem. In the interaction section below you will see the information about flushing the output.
In this problem, you will be playing a game with Hongcow. How lucky of you!
Hongcow has a hidden $ n $ by $ n $ matrix $ M $ . Let $ M_{i,j} $ denote the entry $ i $ -th row and $ j $ -th column of the matrix. The rows and columns are labeled from $ 1 $ to $ n $ .
The matrix entries are between $ 0 $ and $ 10^{9} $ . In addition, $ M_{i,i}=0 $ for all valid $ i $ . Your task is to find the minimum value along each row, excluding diagonal elements. Formally, for each $ i $ , you must find 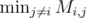.
To do this, you can ask Hongcow some questions.
A question consists of giving Hongcow a subset of distinct indices $ {w_{1},w_{2},...,w_{k}} $ , with $ 1
Input Format
The first line of input will contain a single integer $ n $ ( $ 2
Output Format
To print the final answer, print out the string -1 on its own line. Then, the next line should contain $ n $ integers. The $ i $ -th integer should be the minimum value of the $ i $ -th row of the matrix, excluding elements on the diagonal. Do not forget to flush your answer!
Interaction
To ask a question, print out a single integer $ k $ on its own line, denoting the size of your subset. Then, the next line should contain $ k $ integers $ w_{1},w_{2},...\ w_{k} $ . Note, you must flush your output to get a response.
Hongcow will respond by printing out a line with $ n $ integers. The $ i $ -th integer in this line represents the minimum value of $ M_{i,wj} $ where $ j $ is between $ 1 $ and $ k $ .
You may only ask a question at most $ 20 $ times, otherwise, you will get Wrong Answer.
To flush you can use (just after printing an integer and end-of-line):
- fflush(stdout) in C++;
- System.out.flush() in Java;
- stdout.flush() in Python;
- flush(output) in Pascal;
- See the documentation for other languages.
Hacking To hack someone, use the following format
`
n
M_{1,1} M_{1,2} ... M_{1,n}
M_{2,1} M_{2,2} ... M_{2,n}
...
M_{n,1} M_{n,2} ... M_{n,n}
`Of course, contestant programs will not be able to see this input.
n
M_{1,1} M_{1,2} ... M_{1,n}
M_{2,1} M_{2,2} ... M_{2,n}
...
M_{n,1} M_{n,2} ... M_{n,n}
`Of course, contestant programs will not be able to see this input.
Explanation/Hint
In the first sample, Hongcow has the hidden matrix
`
[
[0, 3, 2],
[5, 0, 7],
[4, 8 ,0],
]
`Here is a more readable version demonstrating the interaction. The column on the left represents Hongcow, while the column on the right represents the contestant. `
3
3
1 2 3
0 0 0
1
3
2 7 0
2
1 2
0 0 4
1
2
3 0 8
1
1
0 5 4
-1
2 5 4
`For the second sample, it is possible for off-diagonal elements of the matrix to be zero.
[
[0, 3, 2],
[5, 0, 7],
[4, 8 ,0],
]
`Here is a more readable version demonstrating the interaction. The column on the left represents Hongcow, while the column on the right represents the contestant. `
3
3
1 2 3
0 0 0
1
3
2 7 0
2
1 2
0 0 4
1
2
3 0 8
1
1
0 5 4
-1
2 5 4
`For the second sample, it is possible for off-diagonal elements of the matrix to be zero.