CF748C Santa Claus and Robot

Santa Claus has Robot which lives on the infinite grid and can move along its lines. He can also, having a sequence of $ m $ points $ p_{1},p_{2},...,p_{m} $ with integer coordinates, do the following: denote its initial location by $ p_{0} $ . First, the robot will move from $ p_{0} $ to $ p_{1} $ along one of the shortest paths between them (please notice that since the robot moves only along the grid lines, there can be several shortest paths). Then, after it reaches $ p_{1} $ , it'll move to $ p_{2} $ , again, choosing one of the shortest ways, then to $ p_{3} $ , and so on, until he has visited all points in the given order. Some of the points in the sequence may coincide, in that case Robot will visit that point several times according to the sequence order. While Santa was away, someone gave a sequence of points to Robot. This sequence is now lost, but Robot saved the protocol of its unit movements. Please, find the minimum possible length of the sequence.

The first line of input contains the only positive integer $ n $ ( $ 1

The only line of input should contain the minimum possible length of the sequence.

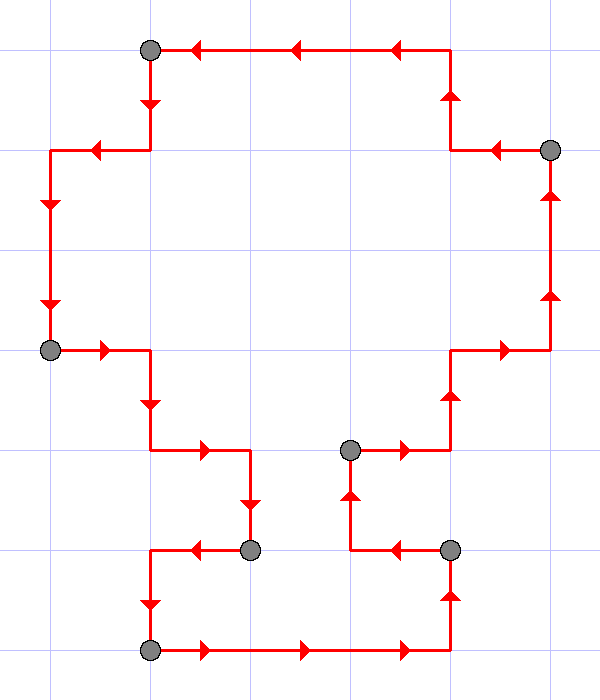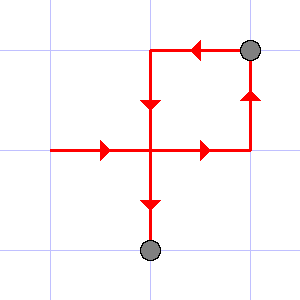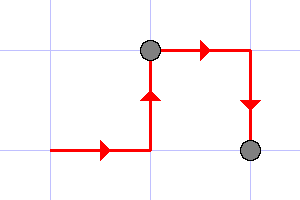
The illustrations to the first three tests are given below.  The last example illustrates that each point in the sequence should be counted as many times as it is presented in the sequence.