CF74C Chessboard Billiard

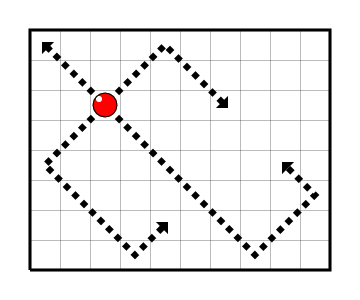
想象一下：有一种叫做台球棋子的球体。它的移动方式类似于国际象棋中的主教。但是有一个区别：当台球碰到棋盘的边界时，它可以从边界反弹并继续移动。 更正式地说，首先选择四个对角方向中的一个，接着台球沿该方向移动。当它到达边界上的某个格子时，台球会从该边界反弹，移动方向发生 90 度转变并继续移动。具体来说，当它到达角落时，台球会被反弹两次，从而沿相反方向移动。在移动过程中，台球可以发生无限次反弹。台球可以在其轨迹上的任意格子停下，这就完成了一次移动。  我们认为若有台球 $a$ 可以到达台球 $b$ 所在的位置，则称 $a$ 能打败 $b$。 请你计算，在 $n \times m$ 的棋盘上，最多能放置多少个两两互不打败对方的台球。

第一行包含两个整数 $n$ 和 $m$（$2 \leq n, m \leq 10^{6}$）。

输出一个整数，表示棋盘上最多能放多少个两两互不打败对方的台球。

由 ChatGPT 5 翻译