CF750D New Year and Fireworks

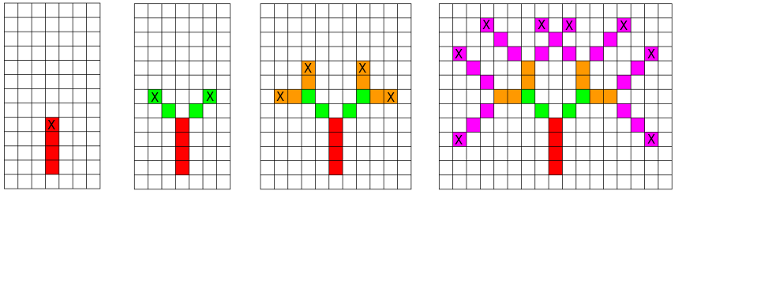
迎接新年的一个传统是向天空发射烟花。通常，发射的烟花会垂直上升一段时间，然后爆炸，分裂成若干部分向不同方向飞行。有时这些部分在经过一段时间后还会再次爆炸，再次分裂成更多的部分，这个过程可以一直持续下去。 Limak 住在一个无限的网格上，他有一支烟花。烟花的行为由递归深度 $n$ 和每一层递归的持续时间 $t_{1}, t_{2}, ..., t_{n}$ 描述。当 Limak 在某个格子发射烟花后，烟花开始向上移动。在经过 $t_1$ 个格子（包括起始格子）后，它会爆炸并分裂成两部分，每一部分分别朝着原方向左转或右转 $45$ 度（见下图示意）。一部分向左上方移动，另一部分向右上方移动。每部分在经过 $t_2$ 个格子后会再次爆炸，并再次分裂成两部分，方向分别改变 $45$ 度。这个过程持续到第 $n$ 层递归为止，此时所有 $2^{n-1}$ 个部分会爆炸并消失，不再产生新的部分。经过若干递归层后，有可能有多个部分同时到达同一个位置，这被允许，且这些部分不会发生碰撞。 在发射烟花之前，Limak 必须确保没有人在烟花可能经过的任何格子里。那么，能否帮他计算一下，有多少个格子会被烟花的某一部分经过至少一次？

第一行包含一个整数 $n$（$1 \leq n \leq 30$），表示递归的总深度。 第二行包含 $n$ 个整数 $t_1, t_2, ..., t_n$（$1 \leq t_i \leq 5$）。在第 $i$ 层，每个 $2^{i-1}$ 个部分在爆炸前会经过 $t_i$ 个格子。

输出一个整数，表示烟花经过至少一次的不同格子的数量。

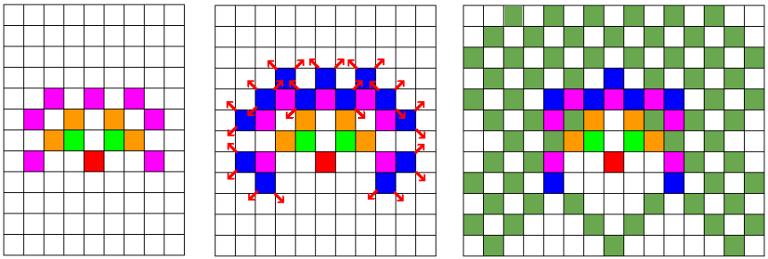
对于第一个样例，下图展示了每一层递归结束后的情形。Limak 从最底部的红色格子发射烟花。它经过 $t_1=4$ 个格子（用红色标记），爆炸并分裂成两部分（后续轨迹用绿色标记）。所有爆炸点用 'X' 标记。最后一张图中有 $4$ 个红色，$4$ 个绿色，$8$ 个橙色以及 $23$ 个粉红色格子。所以，总共被经过的格子数量为 $4+4+8+23=39$。  对于第二个样例，下图展示了经过第 $4$、$5$、$6$ 层递归后的情形。中间的图显示了全部将在下一层移动的部分的方向。  由 ChatGPT 5 翻译