CF750G New Year and Binary Tree Paths

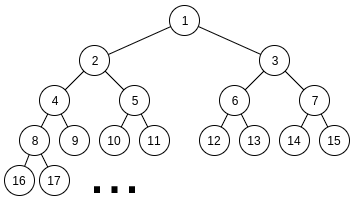
新年树是一棵以结点 $1$ 为根的无限完全二叉树。每个结点 $v$ 拥有两个子结点，编号分别为 $(2·v)$ 和 $(2·v+1)$。  北极熊们都喜欢装饰新年树，Limak 也不例外。不过，由于他还只是只小熊，他只能装饰一条在某两个结点之间的简单路径。当然，这两个结点可以自行选择！现在他想知道有多少对无序结点对 $(u,v)$（满足 $u \leq v$），使得从 $u$ 到 $v$ 的简单路径上所有结点编号之和（包括两个端点）等于 $s$。你能帮他统计这个数量吗？

输入只有一行，包含一个整数 $s$，表示需要的路径结点编号之和。$1 \leq s \leq 10^{15}$。

输出一个整数，表示有多少对无序结点对满足路径编号之和为 $s$。

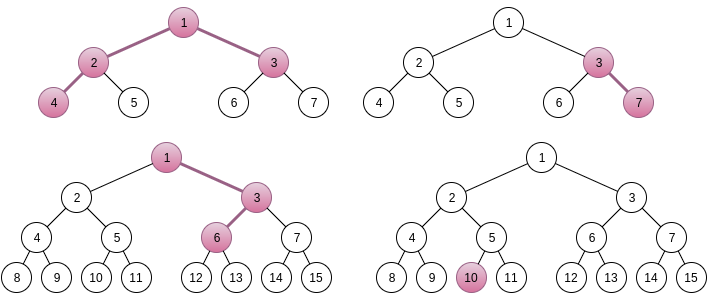
在样例测试中，共有 $4$ 条路径的结点编号之和等于 $10$：  由 ChatGPT 5 翻译