CF755D PolandBall and Polygon

PolandBall 有一个具有 $n$ 个顶点的凸多边形，并且没有三条对角线相交于同一点。PolandBall 决定对它进行改进并画上一些红色线段。 他选择了一个数字 $k$，满足 $gcd(n, k) = 1$。多边形的顶点按顺时针方向从 $1$ 到 $n$ 编号。PolandBall 从顶点 $1$ 开始，重复以下过程共 $n$ 次： 假设你上一次操作结束在顶点 $x$（如果是第一次操作则 $x=1$）。从顶点 $x$ 向顺时针方向的第 $k$ 个顶点画一条新线段。也就是连向顶点 $x+k$ 或 $x+k-n$，取决于哪一个是多边形合法的顶点编号。 你的任务是在每次画线后，计算多边形被分成了多少个区域。一个区域指的是在多边形内部被已画的对角线或多边形边界围成的一个空白区域。

输入包含两个整数 $n$ 和 $k$，满足 $5 \leq n \leq 10^6$，$2 \leq k \leq n-2$，$gcd(n, k) = 1$。

你需要输出 $n$ 个用空格分隔的值。第 $i$ 个值表示画完第 $i$ 条线段之后，多边形被划分成了多少个区域。

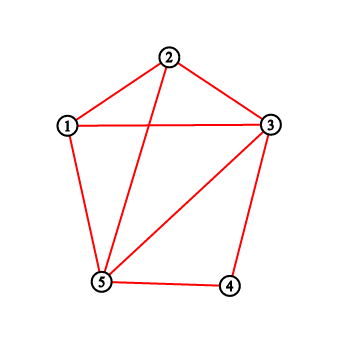
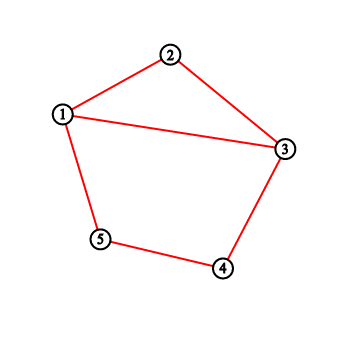
两个整数 $a$ 和 $b$ 的最大公约数（gcd）是能够同时整除 $a$ 和 $b$ 的最大正整数。 对于第一个样例，你应输出 "2 3 5 8 11"。下图分别对应每次画线后的情形。  由 ChatGPT 5 翻译