CF757C Felicity is Coming!

又到了一年一度的 Felicity 节日，你可以看到喜马拉雅地区到处都是庆祝的人们。喜马拉雅地区共有 $n$ 个道馆，第 $i$ 个道馆有 $g_i$ 只宝可梦。此地共有 $m$ 种不同的宝可梦类型，编号为 $1$ 到 $m$。 活动期间开设了一个特殊的进化营，据说可以让宝可梦进化成任意类型。宝可梦进化后的类型可以发生变化，但需遵循如下约束条件：如果两只宝可梦进化前类型相同，进化后它们的类型也必须相同；如果两只宝可梦进化前类型不同，则进化后类型也必须不同。当然，如果进化前后类型未发生变化也是允许的。 形式化地讲，进化方案就是 ${1,2,...,m}$ 的一个排列 $f$，其中 $f(x)=y$ 意味着类型为 $x$ 的宝可梦进化为类型 $y$。 各个道馆馆主都对这个特殊进化营很感兴趣，他们都打算让自己的宝可梦进化。山上的规矩是，对于每个道馆、每种宝可梦类型，所有宝可梦进化前后，该类型宝可梦的数量必须保持不变。现在他们想知道，总共有多少种满足该规矩的不同进化方案。 如果存在至少一个宝可梦类型 $i$，使得两种进化方案 $f_1(i) \neq f_2(i)$，则这两种方案视作不同。 请你计算有多少种不同的合法进化方案，使得所有道馆中的宝可梦全部进化后，每个道馆、每种类型的宝可梦数量均保持不变。由于答案可能很大，请输出对 $10^9+7$ 取模后的结果。

第一行包含两个整数 $n$ 和 $m$（$1\leq n\leq 10^5$，$1\leq m\leq 10^6$），分别表示道馆数量和宝可梦类型数。 接下来 $n$ 行描述每个道馆中的宝可梦。第 $i$ 行以一个整数 $g_i$（$1\leq g_i\leq 10^5$）开头，表示第 $i$ 个道馆的宝可梦数量，之后跟着 $g_i$ 个整数，分别表示这些宝可梦的类型。所有 $g_i$ 之和不超过 $5\cdot 10^5$。

输出合法进化方案的数目，对 $10^9+7$ 取模。

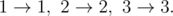
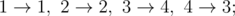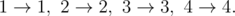
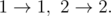
在第一个样例中，唯一可行的进化方案为：  在第二个样例中，$(1,2,3)$ 的任意排列都是可行的。 在第三个样例中，有两种可行的进化方案：   在第四个样例中，唯一可行的进化方案为：  由 ChatGPT 5 翻译