CF757E Bash Plays with Functions

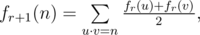
Bash 在成为最伟大的宝可梦大师的旅途中感到有些疲惫，于是他决定休息一下，玩玩函数。 Bash 定义了一个函数 $f_0(n)$，表示将 $n$ 分解为 $p$ 和 $q$ 两个因数，并且满足 $\gcd(p, q) = 1$ 的分解方法数。换句话说，$f_0(n)$ 是满足 $p \cdot q = n$ 且 $\gcd(p, q) = 1$ 的有序正整数对 $(p, q)$ 的数量。 但 Bash 觉得这个函数太简单了，于是他又定义了一系列函数，$f_{r+1}$ 的定义如下：  其中 $(u, v)$ 是任意的有序正整数对，不要求互质。 现在 Bash 想要知道不同 $r$ 和 $n$ 下 $f_r(n)$ 的值。由于答案可能很大，他想要结果对 $10^9 + 7$ 取模。请你帮帮他！

第一行包含一个整数 $q$（$1 \leq q \leq 10^6$），表示 Bash 想要查询的次数。 接下来的 $q$ 行，每行包含两个整数 $r$ 和 $n$（$0 \leq r \leq 10^6$，$1 \leq n \leq 10^6$），表示 Bash 想要知道 $f_r(n)$ 的值。

输出 $q$ 个整数，每行一个答案，分别对应每个 $(r, n)$ 下 $f_r(n)$ 对 $10^9+7$ 取模后的结果。

由 ChatGPT 5 翻译