CF757E Bash Plays with Functions

Bash got tired on his journey to become the greatest Pokemon master. So he decides to take a break and play with functions. Bash defines a function $ f_{0}(n) $ , which denotes the number of ways of factoring $ n $ into two factors $ p $ and $ q $ such that $ gcd(p,q)=1 $ . In other words, $ f_{0}(n) $ is the number of ordered pairs of positive integers $ (p,q) $ such that $ p·q=n $ and $ gcd(p,q)=1 $ . But Bash felt that it was too easy to calculate this function. 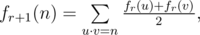So he defined a series of functions, where $ f_{r+1} $ is defined as: Where $ (u,v) $ is any ordered pair of positive integers, they need not to be co-prime. Now Bash wants to know the value of $ f_{r}(n) $ for different $ r $ and $ n $ . Since the value could be huge, he would like to know the value modulo $ 10^{9}+7 $ . Help him!

The first line contains an integer $ q $ ( $ 1

Print $ q $ integers. For each pair of $ r $ and $ n $ given, print $ f_{r}(n) $ modulo $ 10^{9}+7 $ on a separate line.