CF763B Timofey and rectangles

Timofey 收到的生日礼物之一是一本无限平面的彩色书。平面上有 $n$ 个边平行于坐标轴的矩形。所有矩形的边长都是奇数。矩形之间不能相交，但可以相互接触。 请帮助 Timofey 用 $4$ 种不同的颜色给这些矩形上色，使得每两个通过边相互接触的矩形颜色不同，或者判断是否无法做到。 如果两个矩形的交集有正面积，则视为相交；如果存在一对边，它们的交集长度不为零，则视为通过边接触。 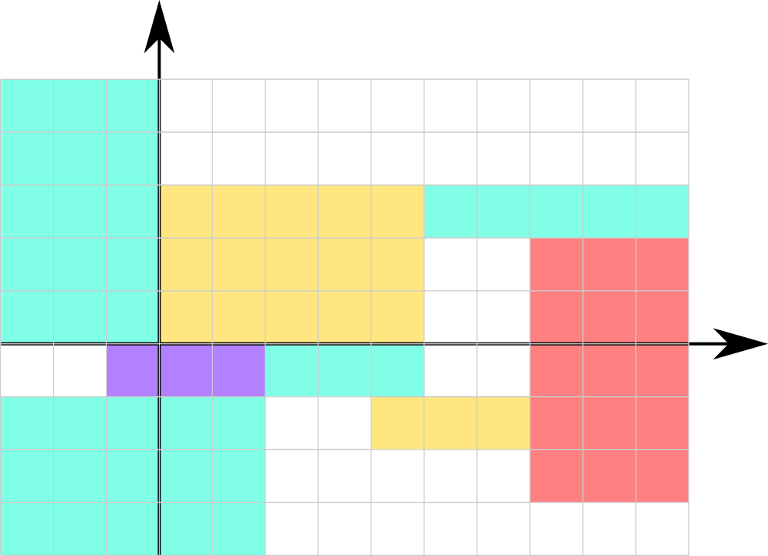 图对应于第一个样例。

第一行包含一个整数 $n$（$1 \le n \le 5 \cdot 10^5$），表示矩形数。 接下来 $n$ 行，每行包含四个整数 $x_1$、$y_1$、$x_2$ 和 $y_2$（$-10^9 \le x_1 < x_2 \le 10^9$，$-10^9 \le y_1 < y_2 \le 10^9$），表示第 $i$ 个矩形的两个对角点坐标$(x_1, y_1)$和$(x_2, y_2)$。 保证所有矩形的边长都是奇数，且两两不相交。

如果无法用 $4$ 种颜色进行合理染色，输出一行 "NO"。 否则，第一行输出 "YES"。接下来 $n$ 行，每行输出一个整数 $c_i$（$1 \le c_i \le 4$），表示第 $i$ 个矩形的颜色编号。

由 ChatGPT 5 翻译