CF765D Artsem and Saunders

Artsem has a friend Saunders from University of Chicago. Saunders presented him with the following problem. Let $ [n] $ denote the set $ {1,...,n} $ . We will also write $ f:[x]→[y] $ when a function $ f $ is defined in integer points $ 1 $ , ..., $ x $ , and all its values are integers from 1 to $ y $ . Now then, you are given a function $ f:[n]→[n] $ . Your task is to find a positive integer $ m $ , and two functions $ g:[n]→[m] $ , $ h:[m]→[n] $ , such that $ g(h(x))=x $ for all 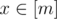, and $ h(g(x))=f(x) $ for all , or determine that finding these is impossible.

The first line contains an integer $ n $ ( $ 1

If there is no answer, print one integer -1. Otherwise, on the first line print the number $ m $ ( $ 1