CF765E Tree Folding

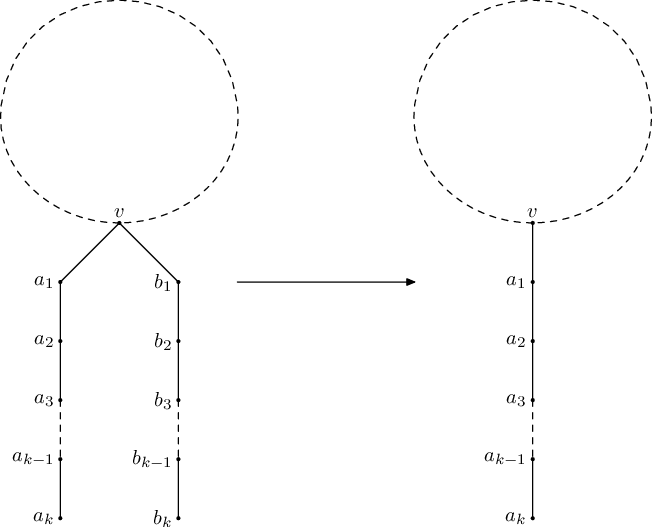
Vanya 想要将一棵树“变小”。他可以多次执行如下操作：选择一个顶点 $v$ 和两条仅有 $v$ 交集并且长度相等的路径，分别记作 $a_{0}=v$，$a_{1}$，...，$a_{k}$ 和 $b_{0}=v$，$b_{1}$，...，$b_{k}$。此外，所有 $a_{1}$，...，$a_{k}$，$b_{1}$，...，$b_{k}$ 必须在树中除了对应路径上的相邻点外，没有其它相邻的顶点。随后，可以将其中一条路径“合并”到另一条路径上，即将 $b_{1}$，...，$b_{k}$ 这些顶点有效地删除：  请你帮助 Vanya 判断能否通过上述一系列操作，将这棵树变为一条路径。如果可以，还需输出该路径的最小可能长度。

第一行输入一个整数 $n$（$2 \leq n \leq 2 \cdot 10^{5}$），表示顶点数。 接下来的 $n-1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \leq u,v \leq n$，$u \ne v$），表示树中的一条无向边的两个端点。保证给定的图是一棵树。

如果无法将树变为一条路径，输出 $-1$。否则，输出一条可能路径的最小边数。

在第一个样例中，可以合并路径 $2-1-6$ 和 $2-4-5$，最终得到长度为 $3$ 的路径。 在第二个样例中无法进行任何操作。例如，无法合并路径 $1-3-4$ 和 $1-5-6$，因为顶点 6 还有一个不在这条路径上的邻居 7。 由 ChatGPT 5 翻译