CF765G Math, math everywhere

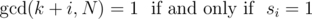
如果你已经走到这一步了，你大概也会跳过一些不必要的传说吧…… 给定一个二进制字符串 $s$，和一个整数 $n$。请你求出在 $0 \leq k < N$ 的所有整数 $k$ 中，有多少个满足对于所有 $i=0,1,\ldots,m-1$ 都有：  满足条件的 $k$ 的个数，答案输出对 $10^9 + 7$ 取模。

第一行输入一个仅由 $0$ 和 $1$ 组成的字符串 $s$（$1 \leq |s| \leq 40$）。 第二行输入一个整数 $n$（$1 \leq n \leq 5 \cdot 10^5$）。 接下来的 $n$ 行中，每行包含两个用空格分隔的整数 $p_i$、$\alpha_i$（$1 \leq p_i, \alpha_i \leq 10^9$，$p_i$ 是质数）。所有 $p_i$ 互不相同。

输出一个整数，即满足条件的 $k$ 的数量。

由 ChatGPT 5 翻译