CF768B Code For 1

Jon fought bravely to rescue the wildlings who were attacked by the white-walkers at Hardhome. On his arrival, Sam tells him that he wants to go to Oldtown to train at the Citadel to become a maester, so he can return and take the deceased Aemon's place as maester of Castle Black. Jon agrees to Sam's proposal and Sam sets off his journey to the Citadel. However becoming a trainee at the Citadel is not a cakewalk and hence the maesters at the Citadel gave Sam a problem to test his eligibility. Initially Sam has a list with a single element $n$. Then he has to perform certain operations on this list. In each operation Sam must remove any element $x$, such that $x > 1$, from the list and insert at the same position 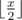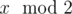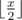$\lfloor \frac{x}{2} \rfloor$, $x \bmod 2$, $\lfloor \frac{x}{2} \rfloor$ sequentially. He must continue with these operations until all the elements in the list are either $0$ or $1$. Now the masters want the total number of $1$s in the range $l$ to $r$ ($1$-indexed). Sam wants to become a maester but unfortunately he cannot solve this problem. Can you help Sam to pass the eligibility test?

The first line contains three integers $n$, $l$, $r$ ($0 \le n < 2^{50}$, $0 \le r - l \le 10^{5}$, $r \ge 1$, $l \ge 1$) – initial element and the range $l$ to $r$. It is guaranteed that $r$ is not greater than the length of the final list.

Output the total number of $ 1 $ s in the range $ l $ to $ r $ in the final sequence.

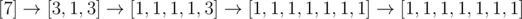
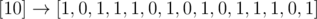
Consider first example: $[1,1,1,1,1,1,1]$ Elements on positions from $ 2 $ -nd to $ 5 $ -th in list is $ [1,1,1,1] $ . The number of ones is $ 4 $ . For the second example: $[1,0,1,1,1,0,1,0,1,0,1,1,1,0,1]$ Elements on positions from $ 3 $ -rd to $ 10 $ -th in list is $ [1,1,1,0,1,0,1,0] $ . The number of ones is $ 5 $ .