CF768F Barrels and boxes

Tarly 有两种不同类型的物品，食物箱和酒桶。他有 $f$ 个食物箱和 $w$ 个酒桶。Tarly 将这些物品分别堆成一堆堆，每一堆只包含食物箱或者酒桶，不能混合。所有的堆依次排成一列，且没有两个食物箱的堆相邻，也没有两个酒桶的堆相邻。 堆的高度定义为该堆中的物品数量。如果两堆的高度不同，或者一堆是食物箱，一堆是酒桶，那么这两个堆被认为是不同的堆。 Jon Snow 不喜欢如下的摆放：如果存在任何一堆酒桶，其高度小于等于 $h$。请计算 Jon Snow 会喜欢的摆放方案的概率，假设所有方案都是等可能的。 如果存在某个 $i$，使得第 $i$ 个堆的类型或高度不同，则两种摆放方案视为不同。

输入的第一行为三个整数 $f$、$w$、$h$，分别表示食物箱数量、酒桶数量，以及 $h$ 的含义（$0 \leq f,w,h \leq 10^{5}$）。保证 $f$ 和 $w$ 至少有一个大于 $0$。

输出一个整数，表示 Jon Snow 喜欢的摆放方案的概率 $p \cdot q^{-1} \bmod (10^9+7)$。概率的表达方式如下图所示： 

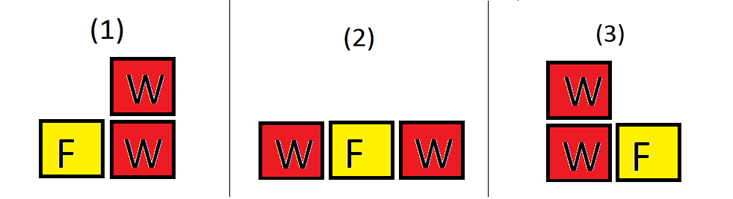
在第一个样例中，$f=1$，$w=1$ 且 $h=1$，只有两种可能的摆放方案，Jon Snow 都不喜欢。 在第二个样例中，$f=1$，$w=2$ 且 $h=1$，共有三种方案，Jon Snow 喜欢第 (1) 和第 (3) 种方案，所以概率为： （即 $2/3$）  由 ChatGPT 5 翻译