CF768G The Winds of Winter

给定一棵有 $n$ 个结点的有根树。夜王移除树中的恰好一个结点及其所有相关的边。这样会将原树分裂成一个森林。被移除的结点不属于这个森林。 森林中每棵树的根是该树中没有父结点的那个结点。我们定义森林的“实力”为森林中最大的一棵树的结点数。 琼恩·雪诺希望最小化森林的实力。为此，他可以至多进行一次如下操作： 他可以将一个结点与其父亲之间的边断开，然后将该结点与森林中的任意其他结点连接（前提是整个森林中的树的数量保持不变）。 对于每个结点 $v$，你需要求出移除结点 $v$ 并允许琼恩·雪诺至多执行一次操作后所得森林“实力”的最小可能值。

第一行包含一个整数 $n$（$1 \leq n \leq 10^5$），表示树中结点的数量。接下来的 $n$ 行，每行包含一对顶点编号 $u_i$ 和 $v_i$（$1 \leq u_i, v_i \leq n$），其中 $u_i$ 是 $v_i$ 的父亲节点。如果 $u_i=0$，则 $v_i$ 是根节点。

输出 $n$ 行，每行包含一个整数。第 $i$ 行应输出移除第 $i$ 个结点并允许琼恩·雪诺至多做一次操作后所得森林“实力”的最小值。

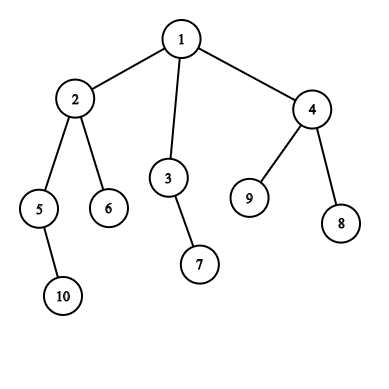
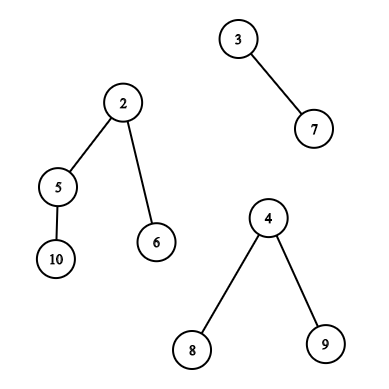
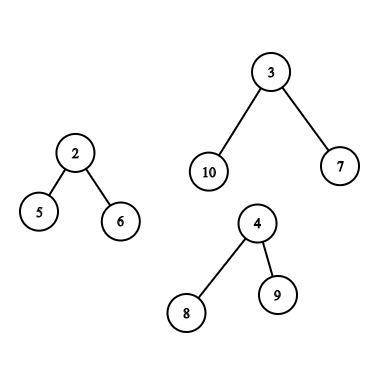
第一组测试样例如下图所示：  当你移除第一个结点时，树会分裂成如下森林，此时“实力”为 $4$：  琼恩·雪诺将结点 $10$ 的父节点从 $5$ 改为 $3$ 后，森林的“实力”变为 $3$：  由 ChatGPT 5 翻译