CF76A Gift
题目描述
奥林匹亚王国由 $N$ 座城市和 $M$ 条双向道路组成。每条道路恰好连接两座城市,不同的城市之间可以有多条道路。还可能存在连接同一座城市自身的自环。
所有道路上都不断被强盗劫掠。过了一段时间,强盗们对劫道产生了厌倦,于是提出让国王用金币和银币作为贿赂来换取安宁。协议中列出了限制条件:对于每条道路,已知 $g_i$ ——让强盗停止在该道路劫掠所需的最少金币数,以及 $s_i$ ——所需的最少银币数。也就是说,如果礼物中包含 $a$ 个金币和 $b$ 个银币,那么对于所有满足 $g_i \leq a$ 且 $s_i \leq b$ 的道路,强盗都会停止劫掠。
不幸的是,国库中既没有金币也没有银币,只有奥林匹亚图格里克(一种货币)。每个金币价值 $G$ 图格里克,每个银币价值 $S$ 图格里克。国王想送出一份尽可能便宜的礼物,使得在所有城市之间都存在一条安全通路。你的任务是计算凑成一条所有城市互相可达的安全路径所需礼物的最小图格里克花费。
输入格式
输入的第一行包含两个整数 $N$ 和 $M$($2 \leq N \leq 200$,$1 \leq M \leq 50000$),分别表示城市数量和道路数量。第二行包含两个整数 $G$ 和 $S$($1 \leq G, S \leq 10^9$),分别表示金币与银币的图格里克价格。接下来的 $M$ 行,每行包括四个整数 $x_i, y_i, g_i, s_i$,其中 $x_i$ 与 $y_i$ 表示道路连接的两座城市,$g_i$ 表示在这条道路上停止劫掠的最少金币,$s_i$ 表示所需的最少银币($1 \leq x_i, y_i \leq N$,$1 \leq g_i, s_i \leq 10^9$)。城市编号从 $1$ 到 $N$。两座城市之间可能有多条道路,可能存在自环。
输出格式
输出所需礼物的最小图格里克花费。如果不存在满足要求的礼物方案,则输出下图所示内容:
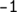
说明/提示
由 ChatGPT 5 翻译