CF771C Bear and Tree Jumps

A tree is an undirected connected graph without cycles. The distance between two vertices is the number of edges in a simple path between them. Limak is a little polar bear. He lives in a tree that consists of $ n $ vertices, numbered $ 1 $ through $ n $ . Limak recently learned how to jump. He can jump from a vertex to any vertex within distance at most $ k $ . For a pair of vertices $ (s,t) $ we define $ f(s,t) $ as the minimum number of jumps Limak needs to get from $ s $ to $ t $ . Your task is to find the sum of $ f(s,t) $ over all pairs of vertices $ (s,t) $ such that $ s \lt t $ .

The first line of the input contains two integers $ n $ and $ k $ ( $ 2

Print one integer, denoting the sum of $ f(s,t) $ over all pairs of vertices $ (s,t) $ such that $ s \lt t $ .

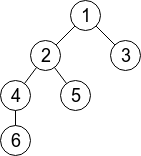In the first sample, the given tree has $ 6 $ vertices and it's displayed on the drawing below. Limak can jump to any vertex within distance at most $ 2 $ . For example, from the vertex $ 5 $ he can jump to any of vertices: $ 1 $ , $ 2 $ and $ 4 $ (well, he can also jump to the vertex $ 5 $ itself). There are 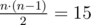 pairs of vertices $ (s,t) $ such that $ s \lt t $ . For $ 5 $ of those pairs Limak would need two jumps: $ (1,6),(3,4),(3,5),(3,6),(5,6) $ . For other $ 10 $ pairs one jump is enough. So, the answer is $ 5·2+10·1=20 $ . In the third sample, Limak can jump between every two vertices directly. There are $ 3 $ pairs of vertices $ (s\lt t) $ , so the answer is $ 3·1=3 $ .