CF771C Bear and Tree Jumps
题目描述
一棵树是一个无环的连通无向图。两个顶点之间的距离是它们之间一条简单路径上的边的数量。
Limak 是一只小北极熊。他住在一棵包含 $n$ 个顶点的树上,顶点编号为 $1$ 到 $n$。
Limak 最近学会了跳跃。他可以从一个顶点跳到距离至多 $k$ 的任意一个顶点。
对于一对顶点 $(s,t)$,记 $f(s,t)$ 为 Limak 从 $s$ 跳到 $t$ 所需的最小跳跃次数。你的任务是求所有满足 $s
输入格式
输入的第一行包含两个整数 $n$ 和 $k$($2 \leq n \leq 200000$,$1 \leq k \leq 5$),分别表示树的顶点数和允许的最大跳跃距离。
接下来的 $n-1$ 行,每行包含两个整数 $a_i$ 和 $b_i$($1 \leq a_i, b_i \leq n$),表示第 $i$ 条边连接的两个顶点的编号。
保证所给的边构成一棵树。
输出格式
输出一个整数,表示所有满足 $s < t$ 的顶点对 $(s,t)$ 的 $f(s,t)$ 的和。
说明/提示
在第一个样例中,给出的树有 $6$ 个顶点,见下图。Limak 可以跳到距离至多 $2$ 的任意顶点。例如,从顶点 $5$ 可以跳到顶点 $1$、$2$ 和 $4$(当然,也可以跳到 $5$ 本身)。
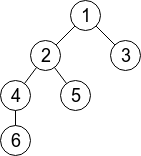
共有 $15$ 组顶点对 $(s,t)$ 满足 $s