CF771E Bear and Rectangle Strips
题目描述
Limak 有一个由 $2$ 行 $n$ 列组成的网格。第 $i$ 行第 $j$ 列的单元格里有一个整数 $t_{i,j}$,可能为正、负或零。
一个非空的矩形被称为“好”(nice),当且仅当其中所有单元格的数字之和等于 $0$。
Limak 想要选择一些“好”矩形作为礼物送给朋友。任意两个被选中的矩形不能有公共单元格。Limak 最多能选择多少个互不相交的“好”矩形?
输入格式
输入的第一行为一个整数 $n$($1 \leq n \leq 300000$),表示网格有 $n$ 列。
接下来的两行描述网格中的数字。第 $i$ 行包含 $n$ 个整数 $t_{i,1}, t_{i,2}, \ldots, t_{i,n}$($-10^9 \leq t_{i,j} \leq 10^9$)。
输出格式
输出一个整数,表示最多能选取多少个互不相交的“好”矩形。
说明/提示
在第一个样例中,有 4 个“好”矩形:
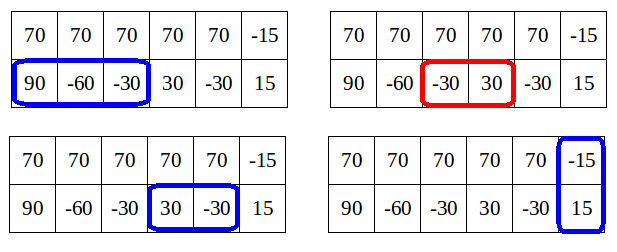
Limak 不能选择全部,因为它们不互不相交。他应该选择被蓝色方框标出的 3 个“好”矩形。
在第二个样例中,最优的做法是选择所有单元格为 $0$ 的单格矩形,共 6 个。
在第三个样例中,唯一的“好”矩形是整个网格(所有数字之和为 $0$)。显然,最多能选 1 个“好”矩形,因此答案是 $1$。
由 ChatGPT 5 翻译