CF772B Volatile Kite
题目描述
给定一个 $ n $ 个顶点的凸多边形 $ P $,顶点依次为 $ p_{1},p_{2},...,p_{n} $。顶点 $ p_{i} $ 在平面上的坐标为 $ (x_{i},y_{i}) $。这些顶点按顺时针顺序给出。
你可以选择一个实数 $ D $,并将多边形的每个顶点都移动至距离其原位置不超过 $ D $ 的任意位置。
请你求出最大的 $ D $,使得无论如何移动各顶点,只要移动距离不超过 $ D $,多边形始终不会自相交,并且始终保持凸多边形。
输入格式
第一行为一个整数 $ n $($ 4 \leq n \leq 1000 $),表示顶点个数。
接下来的 $ n $ 行,每行包含两个整数 $ x_{i},y_{i} $($ -10^{9} \leq x_{i},y_{i} \leq 10^{9} $),表示第 $ i $ 个顶点的坐标。这些点保证按顺时针顺序给出,并且组成严格凸多边形(特别地,任意连续三个点不会共线)。
输出格式
输出一个实数 $ D $,即所求最大的实数,使得无论如何移动各顶点,且移动距离不超过 $ D $,多边形始终保持凸性。
你的答案将被认为正确,当且仅当它的绝对误差或相对误差不超过 $ 10^{-6} $。
具体来说,假设你的答案为 $ a $,标准答案为 $ b $,检查器将判断如下条件是否成立:
$$
\frac{|a-b|}{\max(1,|b|)} \leq 10^{-6}
$$
说明/提示
以下是第一个样例的示意图:
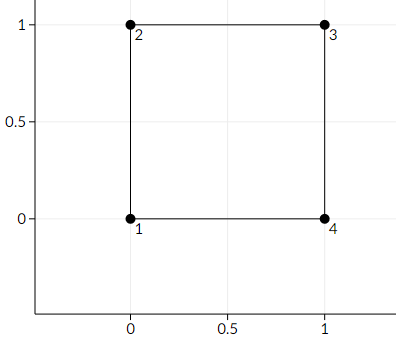
以下是使多边形变为非凸的一个例子:
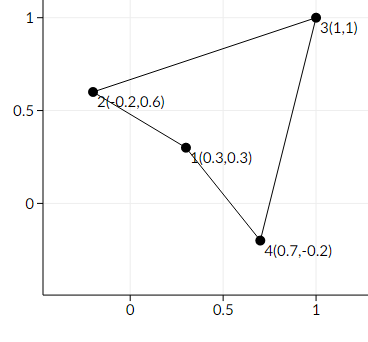
这不是最优解,因为最大移动距离为 $ \approx 0.4242640687 $,而实际上只需最多移动 $ \approx 0.3535533906 $ 就能使多边形失去凸性。
由 ChatGPT 5 翻译