CF772B Volatile Kite
Description
You are given a convex polygon $ P $ with $ n $ distinct vertices $ p_{1},p_{2},...,p_{n} $ . Vertex $ p_{i} $ has coordinates $ (x_{i},y_{i}) $ in the 2D plane. These vertices are listed in clockwise order.
You can choose a real number $ D $ and move each vertex of the polygon a distance of at most $ D $ from their original positions.
Find the maximum value of $ D $ such that no matter how you move the vertices, the polygon does not intersect itself and stays convex.
Input Format
The first line has one integer $ n $ ( $ 4
Output Format
Print one real number $ D $ , which is the maximum real number such that no matter how you move the vertices, the polygon stays convex.
Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-6} $ .
Namely, let's assume that your answer is $ a $ and the answer of the jury is $ b $ . The checker program will consider your answer correct if 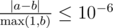.
Explanation/Hint
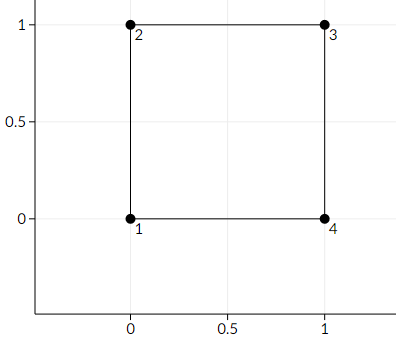
Here is a picture of the first sample
Here is an example of making the polygon non-convex.
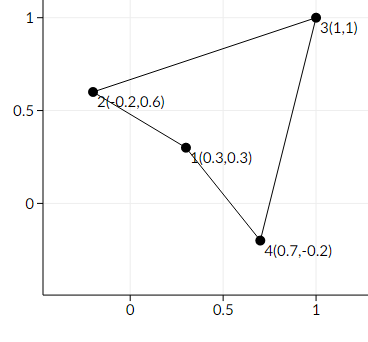
This is not an optimal solution, since the maximum distance we moved one point is $ ≈0.4242640687 $ , whereas we can make it non-convex by only moving each point a distance of at most $ ≈0.3535533906 $ .