CF772E Verifying Kingdom

这是一个交互题。 评测器有一棵隐藏的、有 $n$ 个叶子的有根满二叉树。一棵满二叉树是指，每个节点要么有 $0$ 个孩子，要么有 $2$ 个孩子。拥有 $0$ 个孩子的节点称为树的叶子节点。因为是满二叉树，所以树中共有 $2n-1$ 个节点。评测器的树的叶子节点被依次标号为 $1$ 到 $n$。你需要重建出一棵与评测器的树同构的树。为此，你可以进行若干次询问。 每次询问，你需要输出任意三个互不相同的叶子的编号 $a_1, a_2, a_3$。设某个节点的深度为它到树根的最短距离。记 $LCA(a, b)$ 表示节点 $a$ 和 $b$ 的最近公共祖先中深度最大（距离根最远）的那个节点。 考虑 $X=LCA(a_1, a_2), Y=LCA(a_2, a_3), Z=LCA(a_3, a_1)$。评测器会告诉你这三个节点中哪一个深度最大。注意，这对二叉树来说，深度最大的那个节点是唯一确定的，不会出现平局。 更具体地说，如果 $X$（或 $Y$，$Z$）拥有最大深度，则评测器回复字符串 "X"（或 "Y"，"Z"）。 你最多只能询问 $10·n$ 次。

输入的第一行包含一个整数 $n$（$3 \leq n \leq 1000$），表示树的叶子数。

当你准备好输出答案时，先输出一行 "-1"。接下来一行输出 $2n-1$ 个整数，第 $i$ 个整数表示第 $i$ 个节点的父亲节点编号，如果它是根节点，则为 $-1$。 你的输出只要与评测器的树同构即可，叶子的编号不必一定为 $1$ 到 $n$。这里，“同构”指存在一个排列 $π$，使得评测器树中 $i$ 是 $j$ 的父亲节点，当且仅当你构造的树中 $π(i)$ 是 $π(j)$ 的父亲节点。

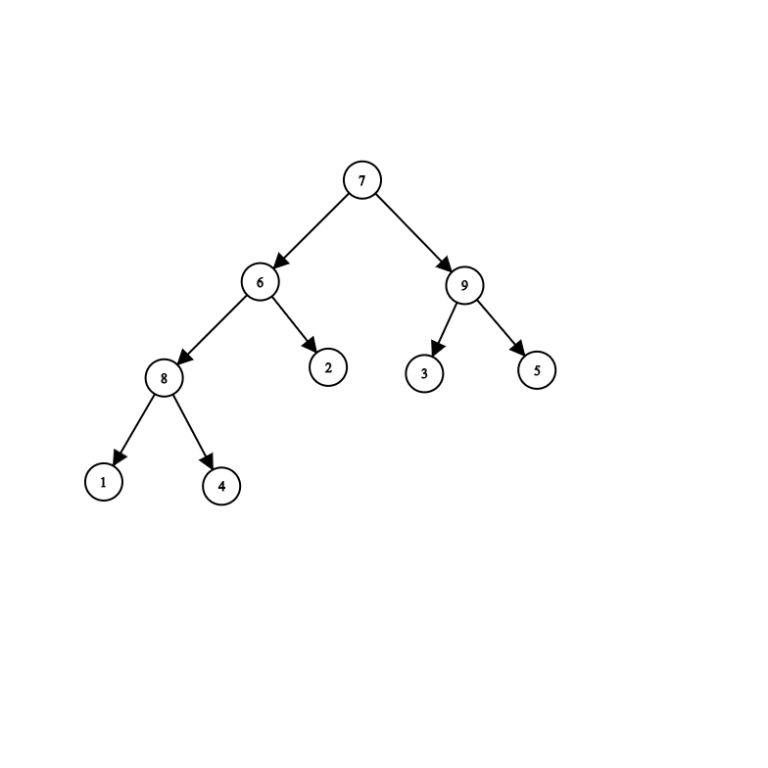
对于第一个样例，评测器的树如下图所示：  下图展示了更清晰的交互格式：  最后一行也可以是 8 6 9 8 9 7 -1 6 7。 由 ChatGPT 5 翻译