CF773B Dynamic Problem Scoring

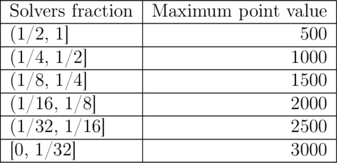
Vasya 和 Petya 参加了一场 Codeforces 编程比赛。这场比赛持续两个小时，共有五道题目。 比赛采用动态计分系统。题目的最高分与你解题的难度有关，具体是根据解决这道题目的人数占总参赛人数的比例来决定的。只要选手有过一次提交，就被视为参赛者。 ！[](https://cdn.luogu.com.cn/upload/vjudge_pic/CF773B/a0f85cbd533a46bf976e07f7a2f9ea90ac93ff77.png) 注意分数区间。例如，有 40 名选手参加比赛，其中 10 人解出某个题目，那么解题比例为 $1/4$，该题目最大分数为 1500 分。 如果题目的最大分数为 $x$，那么从比赛开始到选手正确提交的每分钟，选手都会扣除 $x/250$ 分。例如，题目最大分数是 2000 分，而选手在第 40 分钟提交了答案，那么他将得到 $2000 \times (1 - 40/250) = 1680$ 分。 参赛有 $n$ 位选手，其中包括 Vasya 和 Petya。每位选手对每道题目的提交时间已知，并以分钟为单位记录；如果某题未被解出，则时间记为 -1。 比赛即将结束时，所有选手的提交都通过了预测试，并且没有人尝试黑客攻击。Vasya 认为在最后的两秒钟里不会有新的提交，也没有任何黑客行为，所有提交均会通过系统检测。 然而，Vasya 是个作弊者。他为这场比赛注册了 $10^9 + 7$ 个新账号。Vasya 可以利用这些新账号改变题目的最大分值，提交错误的或者已经解决的题目。需要注意的是，对于未解的题目，他不能提交正确的答案。 Vasya 希望通过这种方式让自己的总得分比 Petya 高。尽管他已经准备好了快速提交脚本，但他不想让作弊行为太过明显，所以希望用尽量少的新账号实现目标。 请你帮 Vasya 找出他需要用多少个新账号才能超越 Petya，或者告诉他如果无法实现这一目标。

第一行包含一个整数 $n$（$2 \leq n \leq 120$），表示包括 Vasya 和 Petya 在内的总参赛者人数。 接下来的 $n$ 行中，每行包含五个整数 $a_{i,1}, a_{i,2}, \ldots, a_{i,5}$（$-1 \leq a_{i,j} \leq 119$），表示比赛开始到第 $i$ 个选手解出第 $j$ 个题目的时间（分钟数），若未解出则为 -1。 保证每位选手至少成功解出一道题。 Vasya 是第一个选手，Petya 是第二个，其余选手顺序无关。

输出一个整数，表示 Vasya 实现超越 Petya 所需的最少新账号数量；如果无法超越，输出 -1。

在第一个示例中，Vasya 的优化策略是利用两个新账号提交最后三道题。这样前两道题的最高分为 1000 分，后三道各为 500 分。Vasya 的总分将是 $980 + 940 + 420 + 360 + 270 = 2970$ 分，而 Petya 为 $800 + 820 + 420 + 440 + 470 = 2950$ 分。 在第二个示例中，Vasya 需用两个新账号的单次失败提交，再用第三个账号的正确提交解决第一道题。这样，所有题目的最高分依次为 500、1500、1000、1500、3000 分。Vasya 最终得分为 2370 分，而 Petya 得分为 2294 分。 在第三个示例中，Vasya 可以借助 27 个新账号为前四道题提交答案，从而让题目变得为 500、500、500、500、2000 分。因第五题的高分，Vasya 能以此战胜仅解出前四题但未能解出第五题的 Petya。 **本翻译由 AI 自动生成**