CF773D Perishable Roads

在 Never 国，有 $n$ 个城市和一个高度发达的道路系统。每一对城市之间恰好有一条双向道路，因此一共有这么多条道路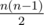：。任意两条道路不会相交，且没有任何一条道路会经过中间城市。Never 国民已经完全掌握了建设隧道与桥梁的技术。 一个独立委员会为 Never 的每一条道路评定了一个正整数，称为道路的“易损度”。道路的易损度越小，驾车行驶起来就越舒适。 现在是 Never 的交通年。已经决定在某个城市建设交通博物馆，并在除此城市以外的每个城市都设置一个指向某个城市的单向路标（路标指向的城市可以是任意一个，不一定是博物馆所在城市）。路标设置需要满足如下重要条件：如果 Never 的任何一位居民从不设博物馆的城市出发，严格按照路标指示前进，那么最终都能到达博物馆所在的城市。 Never 的市民都非常积极乐观。如果一条路线需要经过多条道路，他们会将这条路线的易损度视为所有经过道路的易损度的最小值。 政府尚未决定将博物馆建在哪个城市，因此会考虑所有 $n$ 个城市建馆的方案。政府最关心的是：对于每一个可能的建馆城市，若路标按某种方式设置，使得所有其他城市出发的市民都能沿着路标路线抵达博物馆，且路线的“易损度”总和最小，这一最小值是多少？请帮助他们分别计算出所有 $n$ 个城市作为博物馆时可能得到的最小易损度总和。

第一行包含一个整数 $n$（$2 \leq n \leq 2000$），表示 Never 国的城市数量。 接下来 $n-1$ 行描述道路网络。第 $i$ 行包含 $n-i$ 个整数。第 $i$ 行的第 $j$ 个整数表示城市 $i$ 和城市 $i+j$ 之间的道路的易损度。 所有道路的易损度均在 $1$ 到 $10^9$ 之间。

对于每一个城市（按编号从 $1$ 到 $n$），输出当其作为博物馆城市时，所有其他城市的最小可能路线易损度之和，每行输出一个答案。

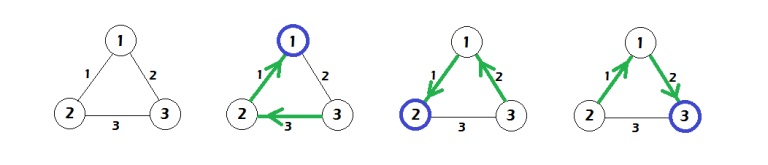
第一个样例可以参考下图。图中从左到右分别表示初始的道路网络，以及将博物馆建在城市 1、2、3 时路标的最优指向。蓝色圆圈代表博物馆所在的城市，绿色箭头表示路标的方向。 例如将博物馆建在城市 3 时，则城市 1 的路标需指向城市 3，城市 2 的路标指向城市 1。那么从城市 1 到城市 3 的路径易损度为 $2$，从城市 2 到城市 3 的路径易损度为 $1$，两者之和为 $3$。  由 ChatGPT 5 翻译