CF774G Perfectionist Arkadiy

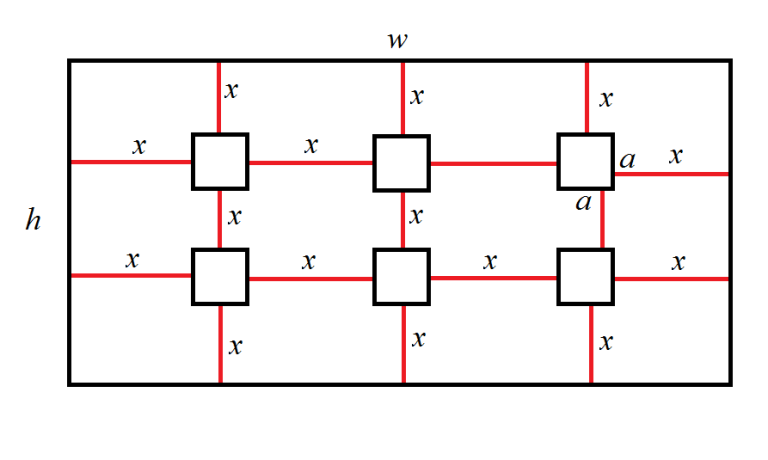
Arkadiy 有许多大小为 $a \times a$ 的正方形照片。他想把其中一些贴在一个大小为 $h \times w$ 的长方形墙上。 Arkadiy 要贴的照片必须排成一个矩形网格，且相邻的竖直和水平照片之间的间距、以及照片外围一行（列）与墙边缘的距离都必须相等，都为 $x$，其中 $x$ 是某个非负实数。下图说明了这一要求。  Arkadiy 还没有决定要贴多少张照片，但他至少要贴一张。你的任务是，确定在贴照片后能够获得的最小 $x$ 的值；或者如果无法贴出满足所有条件的照片方案，需要输出 -1。假设 Arkadiy 拥有足够多的照片，可以任选合法方案。 注意 Arkadiy 至少要贴一张照片。照片不能重叠，必须完全在墙上，并且边与墙边平行。

第一行包含三个整数 $a$、$h$ 和 $w$（$1 \leq a, h, w \leq 10^{9}$），分别表示照片的边长、墙的高度和墙的宽度。

输出一个非负实数，表示贴完所有照片后可以获得的最小 $x$。答案的相对或绝对误差不得超过 $10^{-6}$。 如果无法贴出满足要求的正数数量的照片，输出 $-1$。

在第一个例子中，Arkadiy 可以贴 $7$ 行，每行 $5$ 张照片，因此最小 $x$ 等于 $0.5$。 在第二个例子中，Arkadiy 只能贴 $1$ 张照片并且完全用满墙面，因此最小 $x$ 等于 $0$。 在第三个例子中，无法贴出符合条件的照片，因此输出 -1。 由 ChatGPT 5 翻译