CF776E The Holmes Children

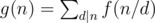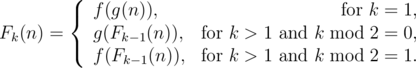Holmes 家的孩子们正在争论谁才是他们中最聪明的人。 Mycroft 让 Sherlock 和 Eurus 求 $ f(n) $ 的值，其中 $ f(1)=1 $，对于 $ n\geq 2 $，$ f(n) $ 是满足 $ x+y=n $ 且 $ \gcd(x,y)=1 $ 的不同有序正整数对 $ (x,y) $ 的个数。整数 $ \gcd(a,b) $ 表示 $ a $ 与 $ b $ 的最大公约数。 Sherlock 说解这个太简单，转而让 Mycroft 来求下式的值：。求和范围是 $ d $ 为所有 $ n $ 的正整数约数。 Eurus 一直在旁边默默看着，最后提出了一个让 Sherlock 和 Mycroft 都惊讶的问题。 她递归地定义了一个 $ k $-复合函数 $ F_{k}(n) $，如下所示： 她想让他们计算 $ F_{k}(n) $ 模 $ 1000000007 $ 的结果。

输入包含一行，包括两个用空格分隔的整数 $ n $（$ 1\leq n\leq 10^{12} $）和 $ k $（$ 1\leq k\leq 10^{12} $），表示 Eurus 要 Sherlock 和 Mycroft 求 $ F_{k}(n) $ 模 $ 1000000007 $ 的值。

输出一个整数，表示 $ F_{k}(n) $ 模 $ 1000000007 $ 的值。

在第一个样例中，有 $ 6 $ 个不同的有序数对 $ (1,6) $、$ (2,5) $、$ (3,4) $、$ (4,3) $、$ (5,2) $ 和 $ (6,1) $ 满足 $ x+y=7 $ 且 $ \gcd(x,y)=1 $。因此，$ f(7)=6 $。所以 $ F_{1}(7)=f(g(7))=f(f(7)+f(1))=f(6+1)=f(7)=6 $。 由 ChatGPT 5 翻译