CF792D Paths in a Complete Binary Tree

$ T $ is a complete binary tree consisting of $ n $ vertices. It means that exactly one vertex is a root, and each vertex is either a leaf (and doesn't have children) or an inner node (and has exactly two children). All leaves of a complete binary tree have the same depth (distance from the root). So $ n $ is a number such that $ n+1 $ is a power of $ 2 $ . In the picture you can see a complete binary tree with $ n=15 $ . 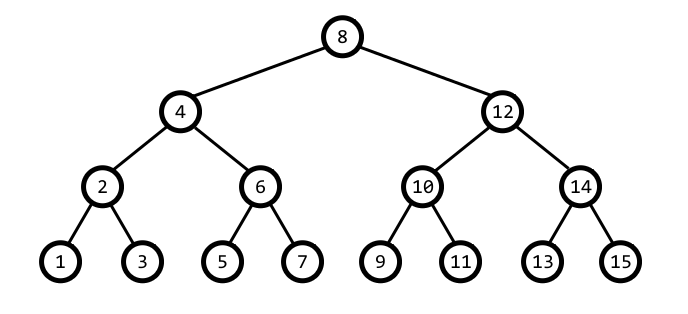Vertices are numbered from $ 1 $ to $ n $ in a special recursive way: we recursively assign numbers to all vertices from the left subtree (if current vertex is not a leaf), then assign a number to the current vertex, and then recursively assign numbers to all vertices from the right subtree (if it exists). In the picture vertices are numbered exactly using this algorithm. It is clear that for each size of a complete binary tree exists exactly one way to give numbers to all vertices. This way of numbering is called symmetric. You have to write a program that for given $ n $ answers $ q $ queries to the tree. Each query consists of an integer number $ u_{i} $ ( $ 1

The first line contains two integer numbers $ n $ and $ q $ ( $ 1

Print $ q $ numbers, $ i $ -th number must be the answer to the $ i $ -th query.