CF792D Paths in a Complete Binary Tree

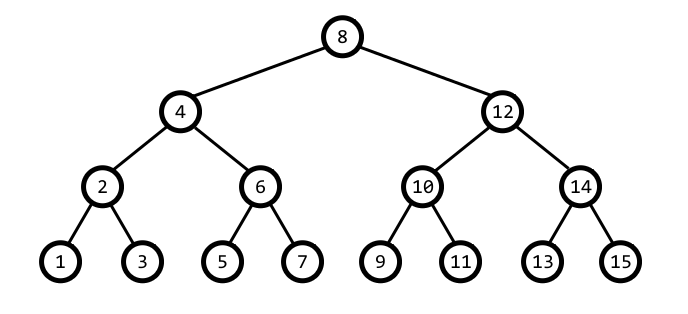
$T$ 是一棵包含 $n$ 个顶点的完美二叉树。这意味着恰好有一个根节点，并且每个节点要么是叶子节点（没有孩子），要么是内节点（有且仅有两个孩子）。完美二叉树的所有叶子节点的深度（从根到该节点的距离）相同。所以 $n$ 满足 $n+1$ 是 $2$ 的幂。 下图展示了一棵 $n=15$ 的完美二叉树。  节点编号方式采用一种特殊的递归方法：对当前节点（如果不是叶子）递归编号左子树的所有节点，然后给当前节点编号，最后递归编号右子树的所有节点（如果存在）。上图的节点编号方式正是使用该算法。可以看出，对于每一种规模的完美二叉树，唯一的一种给所有节点编号的方法。这种编号方法称为“对称编号”。 现在，给定 $n$，你需要为这棵树回答 $q$ 个询问。 每个询问包含一个整数 $u_{i}$（$1 \le u_{i} \le n$）和一个字符串 $s_{i}$，其中 $u_{i}$ 表示起点节点编号，而 $s_{i}$ 表示从该节点出发的一条路径。字符串 $s_{i}$ 只包含 'L'、'R' 和 'U'，分别表示向左儿子、右儿子和父亲节点走。对 $s_{i}$ 应从左到右依次处理，初始位置为 $u_{i}$ 节点。如果某个操作无法进行（如叶子的左儿子或右儿子、根节点向上），则跳过该操作。最终输出路径结束时所停留的节点编号。 例如，如果 $u_{i}=4$，$s_{i}$ 为 “UURL”，那么答案是 $10$。

第一行包含两个整数 $n$ 和 $q$（$1 \le n \le 10^{18}$，$q \ge 1$）。$n$ 满足 $n+1$ 是 $2$ 的幂。 接下来的 $2q$ 行描述所有询问，每一组询问包含两行。第一行为 $u_{i}$（$1 \le u_{i} \le n$），第二行为非空字符串 $s_{i}$。$s_{i}$ 只包含 'L'、'R' 和 'U'，且非空。 保证所有 $s_{i}$ 长度之和不超过 $10^5$。

输出 $q$ 行，每行一个整数，第 $i$ 行表示第 $i$ 个询问的答案。

由 ChatGPT 5 翻译