CF793C Mice problem

分析员 Igor 在工作时睡着了，做了一个奇怪的梦。在梦中，他的桌子上挤满了电脑鼠标，所以他买了一个捕鼠器来抓这些鼠标。 桌子可以看作一个无限大的平面，捕鼠器是一个长方形，其边平行于坐标轴，对角线的两个顶点分别为 $ (x_{1},y_{1}) $ 和 $ (x_{2},y_{2}) $。 Igor 想要抓住所有的鼠标。他分析了鼠标的行为，发现每只鼠标都以恒定速度沿直线移动，第 $i$ 只鼠标的速度为 $ (v_{i}^{x},v_{i}^{y}) $，即任意 $1$ 秒内，其 $x$ 坐标增加 $v_{i}^{x}$ 单位，$y$ 坐标增加 $v_{i}^{y}$ 单位。最开始捕鼠器是开着的，所以鼠标可以自由地在桌上移动。Igor 可以在任意时刻关闭捕鼠器，关闭时能抓住所有严格处于捕鼠器内部的鼠标。 Igor 梦中也很忙，于是希望你编写一个程序：给出捕鼠器的坐标，每只鼠标的初始坐标和速度，判断他最早能在什么时候关闭捕鼠器，从而一次性抓住所有鼠标。注意，Igor 只能关一次捕鼠器。

第一行包含一个整数 $n$（$1 \leq n \leq 100000$），表示桌上有多少只电脑鼠标。 第二行包含四个整数 $x_{1}$、$y_{1}$、$x_{2}$ 和 $y_{2}$（$0 \leq x_{1} \leq x_{2} \leq 100000$，$0 \leq y_{1} \leq y_{2} \leq 100000$），表示捕鼠器对角线两个顶点的坐标。 接下来的 $n$ 行，每行包含四个整数 $r_{i}^{x}, r_{i}^{y}, v_{i}^{x}, v_{i}^{y}$（$0 \leq r_{i}^{x}, r_{i}^{y} \leq 100000$, $-100000 \leq v_{i}^{x}, v_{i}^{y} \leq 100000$），其中 $(r_{i}^{x}, r_{i}^{y})$ 表示第 $i$ 只鼠标的初始位置，$(v_{i}^{x}, v_{i}^{y})$ 表示它的速度。

输出一个非负实数 $t$，表示 Igor 最早可以在第 $t$ 秒关上捕鼠器，使所有鼠标都严格处于捕鼠器内部。如果不存在这样的 $t$，输出 $-1$。 你的答案如果绝对误差或相对误差不超过 $10^{-6}$ 都将被认为是正确的。 形式化地讲，设你的答案为 $a$，标答为 $b$。若满足 $$ \frac{|a-b|}{\max(1, |b|)} \leq 10^{-6} $$ 则视为正确。

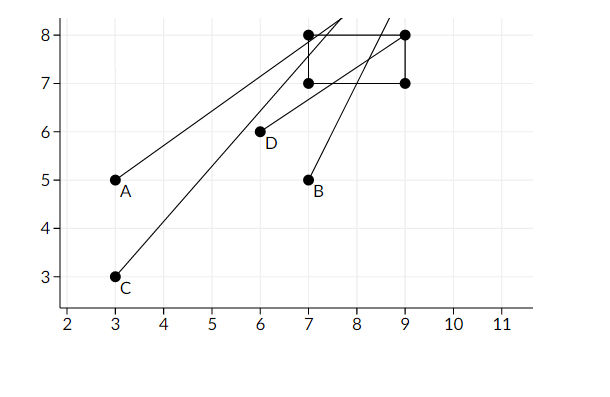
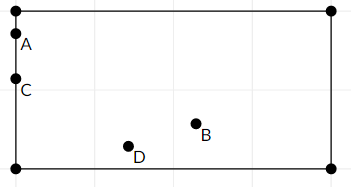
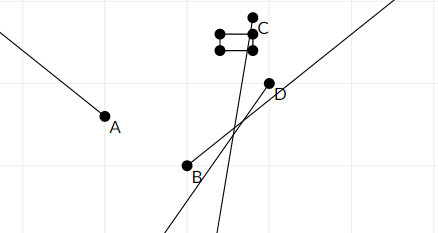
以下是第一个样例的图片： 点 $A, B, C, D$ 表示鼠标的初始位置，线段为它们的运动轨迹。  第一次所有鼠标进入矩形的瞬间如下：  以下是第二个样例的图片：  点 $A, D, B$ 永远不会进入矩形。 由 ChatGPT 5 翻译