CF798C Mike and gcd problem

Mike has a sequence $ A=[a_{1},a_{2},...,a_{n}] $ of length $ n $ . He considers the sequence $ B=[b_{1},b_{2},...,b_{n}] $ beautiful if the $ gcd $ of all its elements is bigger than $ 1 $ , i.e. 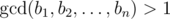. Mike wants to change his sequence in order to make it beautiful. In one move he can choose an index $ i $ ( $ 1

The first line contains a single integer $ n $ ( $ 2

Output on the first line "YES" (without quotes) if it is possible to make sequence $ A $ beautiful by performing operations described above, and "NO" (without quotes) otherwise. If the answer was "YES", output the minimal number of moves needed to make sequence $ A $ beautiful.

In the first example you can simply make one move to obtain sequence $ [0,2] $ with 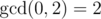. In the second example the $ gcd $ of the sequence is already greater than $ 1 $ .