CF798C Mike and gcd problem

Mike 有一个长度为 $n$ 的序列 $A=[a_1,a_2,\dots,a_n]$。他认为一个序列 $B=[b_1,b_2,\dots,b_n]$ 是优美的，当且仅当其所有元素的 $\gcd$ 大于 $1$，即 $\gcd(b_1,b_2,\dots,b_n)>1$。 Mike 想要对他的序列进行操作来使它变为优美的。每次操作，他可以选择一个下标 $i(1\leqslant i

第一行一个整数 $n(2\leqslant n\leqslant 10^5)$，表示序列 $A$ 的长度。 之后一行，$n$ 个被空格隔开的整数 $a_1,a_2,\dots,a_n(1\leqslant a_i\leqslant10^9)$，表示 $A$ 中的元素。

如果可以使序列变为优美的，第一行输出 `YES`，然后第二行输出最小操作次数。 如果不可能使得序列变为优美的，在第一行输出 `NO`。

In the first example you can simply make one move to obtain sequence $ [0,2] $ with 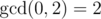. In the second example the $ gcd $ of the sequence is already greater than $ 1 $ .