CF804F Fake bullions

在 Isart，人不会死。有 $n$ 个犯罪团伙。第 $i$ 个团伙里有 $s_i$ 名恶人，其编号从 $0$ 到 $s_i-1$。部分恶人曾参与一次大型矿井抢劫，每人偷得一根金条（这些人将会在输入中给出）。这已经是 $10^{100}$ 年前的事情了，之后所有团伙就逃到了远离城镇的偏僻地区。 这些年里，他们根据有组织的计划，通过复制金条的方式避免被逮捕。他们建立了一个以团伙为节点的比赛型有向图（即任意两个节点间恰有一条有向边，该图在输入中给出）。图中一条从 $u$ 指向 $v$ 的边意味着，在第 $i$ 小时时，团伙 $u$ 的第 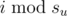 号成员可以向团伙 $v$ 的第 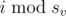 号成员发送一根假金条。如果发送者有金条（无论真伪），并且接收者尚未拥有金条，则可以发送。因此，任意时刻每个恶人手里至多有一根金条，有些是真金条，有些是假金条。 时至今年年初，警察终于找到了这些团伙，但和以往一样，他们依然无法将其抓获。警察于是决定开一家金店，引诱这些恶人出售金条。因此，每个拥有金条的恶人（无论真假）都会尝试出售。如果他手里是真金条，则一定能成功出售；如果是假金条，则有两种可能： - 恶人成功卖出金条。 - 恶人被警察抓获。 一个团伙的“势力值”即为其中成功出售金条的成员人数。当天所有出售结束后，警察会从势力值排名前 $a$ 的团伙中选出 $b$ 个团伙进行逮捕。按照势力值将团伙排序，前 $a$ 名称为“top gangs”（对于势力值相等的团伙，排序可以任意）。考虑所有可能的假金条出售情况以及从 top gangs 中选 $b$ 个团伙的所有方式，计算警察可能逮捕的 $b$ 个团伙集合的种数，结果对 $10^9+7$ 取模。两个集合 $X$ 和 $Y$ 若至少有一个团伙只属于其中之一，则视为不同的集合。

第一行包含四个整数 $n$、$a$ 和 $b$（$1 \leq b \leq a \leq n \leq 5 \times 10^3$），分别表示团伙数，以及题目中的常量 $a$ 和 $b$。 接下来 $n$ 行，每行由 $n$ 个字符 $0$ 或 $1$ 组成，第 $i$ 行第 $j$ 个字符为 $1$ 表示节点 $i$ 有一条指向节点 $j$ 的有向边。保证 $a_{ii}=0$ 且 $a_{ij}+a_{ji}=1$，如果 $i \neq j$。 接下来 $n$ 行，每行以整数 $s_i$ 开头（$1 \leq s_i \leq 2 \times 10^6$），后跟 $s_i$ 个字符 $0$ 或 $1$。第 $j$ 个字符为 $0$ 如果第 $i$ 个团伙的第 $j$ 个成员最初有一根真金条，否则为 $1$。保证所有 $s_i$ 的和不超过 $2 \times 10^6$。

输出一个整数，表示警察可能逮捕 $b$ 个团伙的不同集合的种数，对 $10^9+7$ 取模。

由 ChatGPT 5 翻译