CF809E Surprise me!

Tired of boring dates, Leha and Noora decided to play a game. Leha found a tree with $ n $ vertices numbered from $ 1 $ to $ n $ . We remind you that tree is an undirected graph without cycles. Each vertex $ v $ of a tree has a number $ a_{v} $ written on it. Quite by accident it turned out that all values written on vertices are distinct and are natural numbers between $ 1 $ and $ n $ . The game goes in the following way. Noora chooses some vertex $ u $ of a tree uniformly at random and passes a move to Leha. Leha, in his turn, chooses (also uniformly at random) some vertex $ v $ from remaining vertices of a tree $ (v≠u) $ . As you could guess there are $ n(n-1) $ variants of choosing vertices by players. After that players calculate the value of a function $ f(u,v)=φ(a_{u}·a_{v}) $ $ · $ $ d(u,v) $ of the chosen vertices where $ φ(x) $ is Euler's totient function and $ d(x,y) $ is the shortest distance between vertices $ x $ and $ y $ in a tree. Soon the game became boring for Noora, so Leha decided to defuse the situation and calculate expected value of function $ f $ over all variants of choosing vertices $ u $ and $ v $ , hoping of at least somehow surprise the girl. Leha asks for your help in calculating this expected value. Let this value be representable in the form of an irreducible fraction 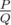. To further surprise Noora, he wants to name her the value 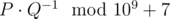. Help Leha!

The first line of input contains one integer number $ n $ $ (2

In a single line print a number equal to $ P·Q^{-1} $ modulo $ 10^{9}+7 $ .

Euler's totient function $ φ(n) $ is the number of such $ i $ that $ 1