CF811D Vladik and Favorite Game
Description
This is an interactive problem.
Vladik has favorite game, in which he plays all his free time.
Game field could be represented as $ n×m $ matrix which consists of cells of three types:
- «.» — normal cell, player can visit it.
- «F» — finish cell, player has to finish his way there to win. There is exactly one cell of this type.
- «\*» — dangerous cell, if player comes to this cell, he loses.
Initially player is located in the left top cell with coordinates $ (1,1) $ .
Player has access to $ 4 $ buttons "U", "D", "L", "R", each of them move player up, down, left and right directions respectively.
But it’s not that easy! Sometimes friends play game and change functions of buttons. Function of buttons "L" and "R" could have been swapped, also functions of buttons "U" and "D" could have been swapped. Note that functions of buttons can be changed only at the beginning of the game.
Help Vladik win the game!
Input Format
First line contains two space-separated integers $ n $ and $ m $ ( $ 1
Output Format
You can press buttons no more than $ 2·n·m $ times.
To press a button you should print "U", "D", "L", "R" in new line. It’s necessary to print newline character and flush output. After flushing buffer you should read answer from input data. Answer is the pair of space-separated integers $ x $ , $ y $ — new position of player. In case, if there is no cell in direction of moving, position will not change. If after any move player lost, in other words player move to dangerous cell, then $ x $ and $ y $ will be equal to $ -1 $ .
If after any move player is in finish or dangerous cell, then you should terminate your program.
To finish output buffer (i. e. for operation flush) right after printing direction and newline you should do next:
- fflush(stdout) in C++
- System.out.flush() in Java
- stdout.flush() in Python
- flush(output) in Pascal
- read documentation for other languages.
Hacks
To perform a hack you should use this format:
`
n m swapLR swapUD
a_1
a_2
...
a_n
`Where $ n $ , $ m $ — number of rows and columns in game field. $ swapLR $ is equal to $ 1 $ in case, when directions "L’’ and "R’’ is swapped, and equal to $ 0 $ otherwise. $ swapUD $ is equal to $ 1 $ , when directions "U’’ and "D’’ is swapped, and equal to $ 0 $ otherwise. $ a_{1},a_{2},...,a_{n} $ — description of corresponding rows of game field.
n m swapLR swapUD
a_1
a_2
...
a_n
`Where $ n $ , $ m $ — number of rows and columns in game field. $ swapLR $ is equal to $ 1 $ in case, when directions "L’’ and "R’’ is swapped, and equal to $ 0 $ otherwise. $ swapUD $ is equal to $ 1 $ , when directions "U’’ and "D’’ is swapped, and equal to $ 0 $ otherwise. $ a_{1},a_{2},...,a_{n} $ — description of corresponding rows of game field.
Explanation/Hint
In first test case all four directions swapped with their opposite directions. Protocol of interaction In more convenient form:
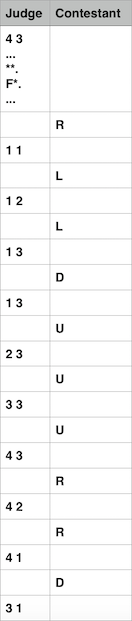
This test could be presenter for hack in following way:
`
4 3 1 1
...
**.
F*.
...
`
4 3 1 1
...
**.
F*.
...
`